【题目】如图,在正方形ABCD中,点E、F在对角线BD上,且BF=DE.
⑴求证:四边形AECF是菱形.
⑵若AB=2,BF=1,求四边形AECF的面积.

参考答案:
【答案】(1)证明见解析;
(2)四边形AECF的面积为4﹣2![]() .
.
【解析】试题分析:(1)根据正方形的性质,可得正方形的四条边相等,对角线平分对角,根据 SAS,可得△ABF与△CBF与△CDE与△ADE的关系,根据三角形全等,可得对应边相等,再根据四条边相等的四边形,可得证明结果;
(2)根据正方形的边长、对角线,可得直角三角形,根据勾股定理,可得AC、EF的长,根据菱形的面积公式,可得答案.
试题解析:(1)证明:正方形ABCD中,对角线BD,
∴AB=BC=CD=DA,
∠ABF=∠CBF=∠CDE=∠ADE=45°.
∵BF=DE,
∴△ABF≌△CBF≌△DCE≌△DAE(SAS).
AF=CF=CE=AE
∴四边形AECF是菱形;
(2)∵AB=2,∴AC=BD=![]()
∴OA=OB=![]() =2.
=2.
∵BF=1,
∴OF=OB-BF=2-1.
∴S四边形AECF=![]() ACEF=
ACEF=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】重阳节期间,某单位组织本单位退休职工前去距离商丘480千米的信阳鸡公山登高旅游,由于人数较多,共租用甲、乙两辆长途汽车沿同一路线赶赴景点.图中的折线、线段分别表示甲、乙两车所走的路程y甲(千米),y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题:
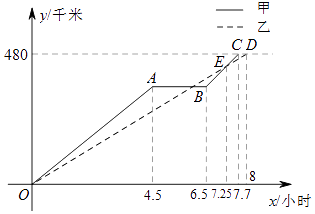
(1)由于汽车发生故障,甲车在途中停留了小时;
(2)甲车排除故障后,立即提速赶往景点.请问甲车在排除故障时,距出发点的路程是多少千米?
(3)为了保证及时联络,甲、乙车在第一次相遇时约定此后两车之间的路程不超过35千米,请通过计算说明,按图象所表示的走法是否符合约定. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC是等边三角形,点D、F分别在线段BC、AB上,∠EFB=60°,DC=EF.
(1)求证:四边形EFCD是平行四边形;
(2)若BF=EF,求证:AE=AD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么这两次拐弯的角度是( )
A. 第一次向右拐40, 第二次向左拐140
B. 第一次向左拐40, 第二次向右拐40
C. 第一次向左拐40, 第二次向左拐140
D. 第一次向右拐40, 第二次向右拐40°
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据提示填空(8分)
如图,EF∥AD,∠1=∠2,∠BAC=80°.将求∠AGD的过程填写完整.

因为EF∥AD
所以∠2=____(____________________________)
又因为∠1=∠2
所以∠1=∠3(______________)
所以AB∥_____(_____________________________)
所以∠BAC+______=180°(_____________________)
因为∠BAC=80° 所以∠AGD=_______
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,△ABC为等边三角形,点D为直线BC上一动点(点D不与B,C重合).以AD为边作菱形ADEF,使∠DAF=60°,连接CF.

初步感知:
(1)如图1,当点D在边BC上时,①求证:∠ADB=∠AFC;②请直接判断结论∠AFC=∠ACB+∠DAC是否成立;
(2)如图2,当点D在边BC的延长线上时,其他条件不变,结论∠AFC=∠ACB+∠DAC是否成立?请写出∠AFC、∠ACB、∠DAC之间存在的数量关系,并写出证明过程;
(3)如图3,当点D在边CB的延长线上时,且点A、F分别在直线BC的异侧,其他条件不变,请补全图形,并直接写出∠AFC、∠ACB、∠DAC之间存在的等量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE把
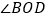 分成两部分;
分成两部分;(1)直接写出图中
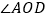 的对顶角为 ,
的对顶角为 ,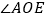 的邻补角为 ;
的邻补角为 ;(2)若
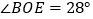 ,且
,且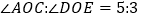 ,求
,求 的度数.
的度数.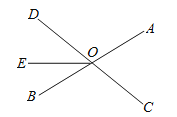
相关试题

