【题目】如图,△ ![]() 三边上的中线
三边上的中线 ![]() 交于点
交于点 ![]() ,若
,若 ![]() ,则图中阴影部分的面积是________.
,则图中阴影部分的面积是________.

参考答案:
【答案】8
【解析】
根据三角形的中线把三角形的面积分成相等的两部分,S△CGE和S△BGF是△ABC面积的![]() .
.
解:∵△ABC的三条中线AD、BE,CF交于点G,
∴S△CGE=S△AGE,S△BGF=S△AGF,S△BDG=S△CDG,
S△ABD=S△BCF=![]() S△ABC=12,
S△ABC=12,
∴S△ABD-S四边形BDGF= S△BCF-S四边形BDGF,
∴S△AGF=S△CDG,
同理可证,
S△CGE=S△AGE=S△BGF=S△BGD=S△BDG=S△CDG,
∵S△ABC=24cm2,
∴S△CGE=S△BGF=![]() ×24=4,
×24=4,
∴S阴影=S△CGE+S△BGF=8.
故答案为8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】工厂准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
 求一只A型节能灯和一只B型节能灯的售价各是多少元?
求一只A型节能灯和一只B型节能灯的售价各是多少元?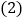 工厂准备购进这两种型号的节能灯共50只,且A型节能灯的数量不多于B型节能灯数量的4倍,当购进A型节能灯m只时,工厂的总费用为w元.
工厂准备购进这两种型号的节能灯共50只,且A型节能灯的数量不多于B型节能灯数量的4倍,当购进A型节能灯m只时,工厂的总费用为w元. 写出
写出 元
元 与
与 只
只 之间的函数关系式,并写出自变量取值范围;
之间的函数关系式,并写出自变量取值范围; 如何购买A、B型节能灯,可以使总费用最少,且总费用最少是多少?
如何购买A、B型节能灯,可以使总费用最少,且总费用最少是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,以
 的AC边为直径作
的AC边为直径作 交斜边AB于点E,连接EO并延长交BC的延长线于点D,作
交斜边AB于点E,连接EO并延长交BC的延长线于点D,作 交BC于点F,连接EF.
交BC于点F,连接EF. 求证:
求证:
 求证:EF是
求证:EF是 的切线;
的切线; 若
若 的半径为3,
的半径为3, ,求AD的长.
,求AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是小章为学校举办的数学文化节没计的标志,在△ABC中,∠ACB=90°,以△ABC的各边为边作三个正方形,点G落在HI上,若AC+BC=6,空自部分面积为10.5,则阴影部分面积为______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC纸片中,∠C=90°,AC=3,BC=4,点D在边BC上,以AD为折痕将△ABD折叠得到△AB’D,AB'与边BC交于点E.若△DEB’为直角三角形,则BD的长是________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类
A
B
C
D
E
出行方式
共享单车
步行
公交车
的士
私家车

根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有 人,其中选择B类的人数有 人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,点B、F、C、E在同一条直线上,AB∥DE,∠A=∠D,BF=EC.
(1)求证:△ABC≌△DEF.
(2)若∠A=120°,∠B=20°,求∠DFC的度数.

相关试题

