Question

【题目】如图，Rt△ABC纸片中，∠C=90°，AC=3，BC=4，点D在边BC上，以AD为折痕将△ABD折叠得到△AB’D，AB'与边BC交于点E．若△DEB’为直角三角形，则BD的长是________．

Answer 1

【答案】1或

【解析】

由勾股定理可求出AB，若△DEB′为直角三角形，则有（1）∠EDB′=90°，（2）∠DEB′=90°两种情况，因此分别画出图形，在第（1）种情况中，由折叠和三角形的内角和可证△ACE∽△BCA，求出CE、AE的长，进而求出DE、EB′，在Rt△DEB′中，设未知数，列方程求解即可，在第（2）种情况中，点E与点C重合，求出EB′，在Rt△DEB′中，由勾股定理列方程求解即可．

解：在Rt△ACB中，

∵ ∠C=90°，AC=3，BC=4，

∴AB=5，

又∵ 以AD为折痕将△ABD折叠得到△ABD，

∴BD=BD，AB=AB=5，

∵△DEB为直角三角形，

∴①如图1所示：当∠BDE=90°时，过B作BF⊥AC交AC延长线于F，

设BD=BD=x，

∴AF=AC+CF=3+x，BF=CD=CB-BD=4-x，

在Rt△AFB中，

∴AF2+BF2=AB2 ，

即(3+x)2+(4-x)2=52 ，

解得：x=1或x=0(舍去)，

∴BD=BD=1，

②如图2所示：当∠BED=90°时，此时点C与点E重合，

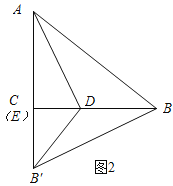
∵AB=5，AC=3，

∴BE=AB-AC=5-3=2，

设BD=BD=y，

∴CD=BC-BD=4-y，

在Rt△BDE中，

∴BE2+DE2=DB2 ，

即(4-y)2+22=y2 ，

解得：y= ，

∴BD=BD= ，

综上所述：BD的长为1或.

故答案为：1或.