【题目】联想三角形外心的概念,我们可引入如下概念. 定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
举例:如图1,若PA=PB,则点P为△ABC的准外心.
(1)应用:如图2,CD为等边三角形ABC的高,准外心P在高CD上,且PD= ![]() AB,求∠APB的度数.
AB,求∠APB的度数. 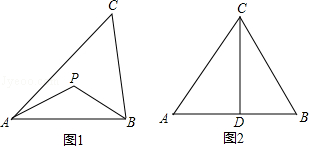
(2)探究:已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上,试探究PA的长.
参考答案:
【答案】
(1)解:①若PB=PC,连接PB,则∠PCB=∠PBC,
∵CD为等边三角形的高,
∴AD=BD,∠PCB=30°,
∴∠PBD=∠PBC=30°,
∴PD= ![]() DB=
DB= ![]() AB,
AB,
与已知PD= ![]() AB矛盾,∴PB≠PC,
AB矛盾,∴PB≠PC,
②若PA=PC,连接PA,同理可得PA≠PC,
③若PA=PB,由PD= ![]() AB,得PD=BD,
AB,得PD=BD,
∴∠APD=45°,
故∠APB=90°
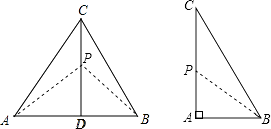
(2)解:∵BC=5,AB=3,
∴AC= ![]() =
= ![]() =4,
=4,
①若PB=PC,设PA=x,则x2+32=(4﹣x)2,
∴x= ![]() ,即PA=
,即PA= ![]() ,
,
②若PA=PC,则PA=2,
③若PA=PB,由图知,在Rt△PAB中,不可能.
故PA=2或 ![]() .
.
【解析】应用:连接PA、PB,根据准外心的定义,分①PB=PC,②PA=PC,③PA=PB三种情况利用等边三角形的性质求出PD与AB的关系,然后判断出只有情况③是合适的,再根据等腰直角三角形的性质求出∠APB=45°,然后即可求出∠APB的度数; 探究:先根据勾股定理求出AC的长度,根据准外心的定义,分①PB=PC,②PA=PC,③PA=PB三种情况,根据三角形的性质计算即可得解.
【考点精析】掌握线段垂直平分线的性质和等腰三角形的性质是解答本题的根本,需要知道垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;等腰三角形的两个底角相等(简称:等边对等角).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某晚报“百姓热线”一周内接到热线电话的统计图,其中有关环境保护问题的电话最多,共70个,请回答下列问题:

(1)本周“百姓热线”共接到热线电话多少个?
(2)有关道路交通问题的电话多少个?
(3)计算其他各类电话的个数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某中学初三年级300名男学生的身体发育情况,从中对20名男学生的身高进行了测量,结果如下:(单位:cm)
175 161 171 176 167 181 161 173 171 177
179 172 165 157 173 173 166 177 169 181
下表是根据上述数据填写的表格的一部分:
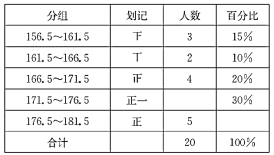
(1)请填写表中未完成的部分;
(2)该校初三年级男学生身高在171.5~176.5(cm)范围内的人数为多少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C、D,PE是⊙O的切线,E为切点,连结AE,交CD于点F.
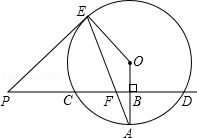
(1)若⊙O的半径为8,求CD的长;
(2)证明:PE=PF;
(3)若PF=13,sinA= ,求EF的长.
,求EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1:y=mx+4m与x轴负半轴、y轴正半轴分别交于A、B两点.
(1)如图(1),当OA=OB时,求直线l1的解析式;
(2)如图(2),当m取不同的值时,点B在y轴正半轴上运动,分别以OB、AB为腰,点B为直角顶点在第一、二象限作等腰直角△OBF和等腰直角△ABE,连接EF交y轴于点P,试猜想PB的长是否为定值?若是,求出其值;若不是,说明理由.
(3)m取不同的值时,点B在y轴正半轴上运动,以AB为腰,点B为直角顶点在第二象限作等腰直角△ABD,满足条件的动点D在直线l2上运动,直线l2与x轴和y轴分别交于F、H两点,若直线l1将△OHF分成面积比为m:1的两部分,求此时直线l1和直线l2的解析式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
 x2+bx+c与y轴交于点C(0,﹣4),与x轴交于点A,B,且B点的坐标为(2,0).
x2+bx+c与y轴交于点C(0,﹣4),与x轴交于点A,B,且B点的坐标为(2,0).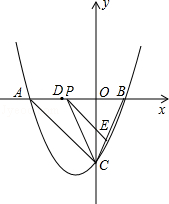
(1)求该抛物线的解析式.
(2)若点P是AB上的一动点,过点P作PE∥AC,交BC于E,连接CP,求△PCE面积的最大值.
(3)若点D为OA的中点,点M是线段AC上一点,且△OMD为等腰三角形,求M点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】今年,市政府的一项实事工程就是由政府投人1000万元资金对城区4万户家庭的老式水龙头和13L抽水马桶进行免费改造.某社区为配合政府完成该项工作,对社区内1200户家庭中的120户进行了随机抽样调查,并汇总成下表:
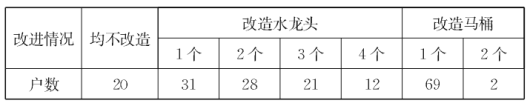
(1)试估计该社区需要对水龙头、马桶进行改造的家庭共有_______户;
(2)改造后,一只水龙头一年大约可节省5t水,一只马桶一年大约可节省15t水,试估计该社区一年共可节约多少吨自来水?
(3)在抽样的120户家庭中,既要改造水龙头又要改造马桶的家庭共有多少户?
相关试题

