【题目】如图,直线l1:y=mx+4m与x轴负半轴、y轴正半轴分别交于A、B两点.
(1)如图(1),当OA=OB时,求直线l1的解析式;
(2)如图(2),当m取不同的值时,点B在y轴正半轴上运动,分别以OB、AB为腰,点B为直角顶点在第一、二象限作等腰直角△OBF和等腰直角△ABE,连接EF交y轴于点P,试猜想PB的长是否为定值?若是,求出其值;若不是,说明理由.
(3)m取不同的值时,点B在y轴正半轴上运动,以AB为腰,点B为直角顶点在第二象限作等腰直角△ABD,满足条件的动点D在直线l2上运动,直线l2与x轴和y轴分别交于F、H两点,若直线l1将△OHF分成面积比为m:1的两部分,求此时直线l1和直线l2的解析式.

参考答案:
【答案】(1)y=x+4;(2)PB的长为定值,理由见解析;(3)直线l1的解析式为:y=![]() x+6-2
x+6-2![]() ,直线l2的解析式为:y=-x+4
,直线l2的解析式为:y=-x+4
【解析】
(1)由直线![]() 解析式,求出A与B坐标,根据OA=OB,求出m的值,即可确定出直线L解析式;
解析式,求出A与B坐标,根据OA=OB,求出m的值,即可确定出直线L解析式;
(2)过点E作EG⊥y轴于G点,先证明△ABO≌△EGB,从而得到BG=4,然后证明△BFP≌△GEP,从而得到BP=GP=![]() BG;
BG;
(3)如图③,由A(-4,0),B(0,4m),得到OA=BG=4,DG=OB=4m,得到点D(-4m,4m+4),于是求得直线![]() 的解析式为:
的解析式为:![]() 根据三角形的面积公式列方程即可得到结论.
根据三角形的面积公式列方程即可得到结论.
解:(1)∵直线l1:y=mx+4m与x轴负半轴、y轴正半轴分别交于A、B两点,
∴A(-4,0),B(0,4m),
由OA=OB,得4m=4,m=1,
∴直线解析式为:y=x+4;
(2)PB的长为定值.
理由:如图②所示:过点E作EG⊥y轴于G点.
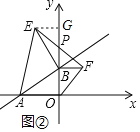
∵△AEB为等腰直角三角形,
∴AB=EB,∠ABO+∠EBG=90°.
∵EG⊥BG,
∴∠GEB+∠EBG=90°.
∴∠ABO=∠GEB.
在△ABO和△EGB中,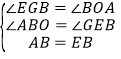 ,
,
∴△ABO≌△EGB.(AAS)
∴BG=AO=4,OB=EG
∵△OBF为等腰直角三角形,
∴OB=BF
∴BF=EG.
在△BFP和△GEP中, ,
,
∴△BFP≌△GEP.(AAS)
∴BP=GP=![]() BG=2是定值;
BG=2是定值;
(3)如图③,
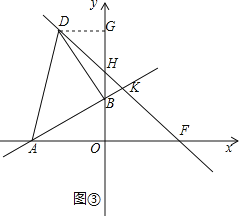
∵A(-4,0),B(0,4m),
由(2)证得OA=BG=4,DG=OB=4m,
∴OG=OB+BG=4m+4,
∴点D(-4m,4m+4),
∵动点D在直线y=-x+4上运动,
∴直线l2的解析式为:y=-x+4,
∴F(4.0),H(0,4),
∴S△OHF=![]() ×4×4=8,
×4×4=8,
设直线l1和直线l2的交点为K,
解![]() 得,
得,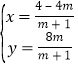 ,
,
∴K(![]() ,
,![]() ),
),
∵直线l1将△OHF分成面积比为m:1的两部分,
∴当S△HBK:S四边形OFKB=m:1时,
S△HBK=![]() (4-4m)
(4-4m)![]() =8×
=8×![]() ,
,
解得:m=![]() ,m=
,m=![]() ,
,
当S△HBK:S四边形OFKB=1:m时,
S△HBK=![]() (4-4m)
(4-4m)![]() =8×
=8×![]() ,
,
解得:m=2,m=0,
∵4m<4,且m≠0,
∴m=![]() ,
,
∴直线l1的解析式为:y=![]() x+6-2
x+6-2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某中学初三年级300名男学生的身体发育情况,从中对20名男学生的身高进行了测量,结果如下:(单位:cm)
175 161 171 176 167 181 161 173 171 177
179 172 165 157 173 173 166 177 169 181
下表是根据上述数据填写的表格的一部分:
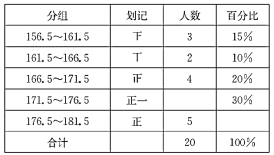
(1)请填写表中未完成的部分;
(2)该校初三年级男学生身高在171.5~176.5(cm)范围内的人数为多少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C、D,PE是⊙O的切线,E为切点,连结AE,交CD于点F.
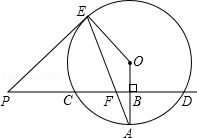
(1)若⊙O的半径为8,求CD的长;
(2)证明:PE=PF;
(3)若PF=13,sinA= ,求EF的长.
,求EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】联想三角形外心的概念,我们可引入如下概念. 定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
举例:如图1,若PA=PB,则点P为△ABC的准外心.
(1)应用:如图2,CD为等边三角形ABC的高,准外心P在高CD上,且PD= AB,求∠APB的度数.
AB,求∠APB的度数. 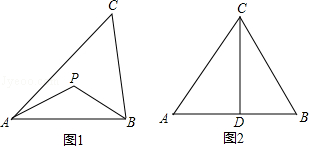
(2)探究:已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上,试探究PA的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
 x2+bx+c与y轴交于点C(0,﹣4),与x轴交于点A,B,且B点的坐标为(2,0).
x2+bx+c与y轴交于点C(0,﹣4),与x轴交于点A,B,且B点的坐标为(2,0).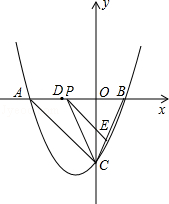
(1)求该抛物线的解析式.
(2)若点P是AB上的一动点,过点P作PE∥AC,交BC于E,连接CP,求△PCE面积的最大值.
(3)若点D为OA的中点,点M是线段AC上一点,且△OMD为等腰三角形,求M点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】今年,市政府的一项实事工程就是由政府投人1000万元资金对城区4万户家庭的老式水龙头和13L抽水马桶进行免费改造.某社区为配合政府完成该项工作,对社区内1200户家庭中的120户进行了随机抽样调查,并汇总成下表:
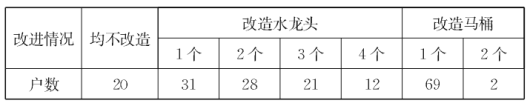
(1)试估计该社区需要对水龙头、马桶进行改造的家庭共有_______户;
(2)改造后,一只水龙头一年大约可节省5t水,一只马桶一年大约可节省15t水,试估计该社区一年共可节约多少吨自来水?
(3)在抽样的120户家庭中,既要改造水龙头又要改造马桶的家庭共有多少户?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据:1,2,6,3,3,下列说法错误的是( )
A.众数是3
B.中位数是6
C.平均数是3
D.方差是2.8
相关试题

