【题目】如图,在平面直角坐标系上,△ABC的顶点A和C分别在x轴、y轴的正半轴上,且AB∥y轴,点B(1,3),将△ABC以点B为旋转中心顺时针方向旋转90°得到△DBE,恰好有一反比例函数y= ![]() 图象恰好过点D,则k的值为( )
图象恰好过点D,则k的值为( ) 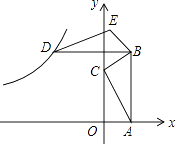
A.6
B.﹣6
C.9
D.﹣9
参考答案:
【答案】B
【解析】解:如图, 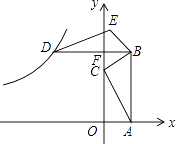
∵△ABC以点B为旋转中心顺时针方向旋转90°得到△DBE,点B(1,3),AB∥y轴,
∴BD=BA=3,∠DBA=90°,
∴BD∥x轴,
∴DF=3﹣1=2,
∴D(﹣2,3).
∵反比例函数y= ![]() 图象恰好过点D,
图象恰好过点D,
∴3= ![]() ,解得k=﹣6.
,解得k=﹣6.
故选B.
先根据旋转的性质得BD=BA=3,∠DBA=90°,则BD∥x轴,易得D(﹣2,3),然后利用待定系数法求反比例函数解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某车间有技术工人85人,平均每天每人可加工甲种部件16个或乙种部件10个,2个甲种部件和3个乙种部件配成一套,问加工甲、乙两种部件各安排多少人才能使每天加工的两种部件刚好配套?并求出加工了多少套?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABE≌△ADC≌△ABC,若∠1∶∠2∶∠3=28∶5∶3,则∠α的度数为( )
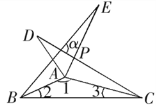
A. 80° B. 100° C. 60° D. 45°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在平面直角坐标系中,抛物线y=﹣
 x2+bx+c与x轴交于点A(﹣4,0),与y轴交于点B(0,4).
x2+bx+c与x轴交于点A(﹣4,0),与y轴交于点B(0,4).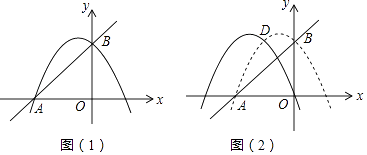
(1)求抛物线的函数解析式;
(2)在x轴上有一点P,点P在直线AB的垂线段为PC,C为垂足,且PC=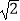 ,求点P的坐标;
,求点P的坐标;
(3)如图(2),将原抛物线向左平移,使平移后的抛物线过原点,与原抛物线交于点D,在平移后的抛物线上是否存在点E,使S△APE=S△ACD?若存在,请求出点E的坐标,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两所学校共82人参加文艺汇演(其中甲校人数多于乙校人数,且甲校人数小于80人),如果两所学校分别购买服装,共付款6060元.
购买服装套数
1~40
41~80
81套及81套以上
每套服装价格
80元
70元
60元
(1)如果甲、乙两所学校联合起来购买服装,那么比各自购买服装一共可以节约多少钱?
(2)甲、乙两所学校各有多少学生参加演出?
(3)如果乙学校单独购买时,服装厂每件服装获利60%,丙学校购买的服装比乙多15套,那么服装厂卖给丙学校服装时共获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从下列四个条件:①
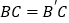 , ②
, ② ,③
,③  ,④
,④ 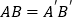 中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( )
中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( )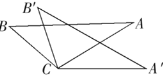
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c的图象的一部分过点A(5,0),对称轴为直线x=1,则下列结论中错误的是( )

A.abc<0
B.当x<1时,y随x的增大而增大
C.4a﹣2b+c<0
D.方程ax2+bx+c=0的根为x1=﹣3,x2=5
相关试题

