【题目】在平面直角坐标中,A (0,5)、B (4,0)、C (2,5),四边形AOBC经过平移后得到四边形A′O′B′C′.

(1) 如图1,若A′(-3,5),四边形AOBC内部一点M(a+b-2,6a-7)经过平移后得到点N(a+2b-7,4b-6),求M点的坐标
(2) 如图2,若四边形AOBC向右平移m个单位长度(m>0).当m为何值时,重叠部分的面积比四边形BB′C′C的面积大
(3) 如图3,若四边形AOBC向上平移2个单位长度,直接写出图中阴影部分的面积.
参考答案:
【答案】(1)![]() ;(2)当
;(2)当![]() 时,重叠部分的面积比四边形BB′C′C的面积大;(3)
时,重叠部分的面积比四边形BB′C′C的面积大;(3)![]()
【解析】
(1)根据对应点的横坐标和纵坐标的变化确定平移方向和平移距离;
(2)用m表示线段长,根据梯形面积公式表示出重叠部分和四边形BB′C′C的面积,根据二者的关系列出不等式求解;
(3)根据平移性质和勾股定理求出OD的长度,由图形特征得出阴影部分的面积等于梯形OBDO的面积,根据梯形面积公式计算.
(1)∵A (0,5),A′(-3,5),
∴四边形AOBC向左平移3个单位得到四边形A′O′B′C′,
∵M(a+b-2,6a-7)对应点为N(a+2b-7,4b-6),
∴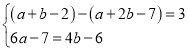 ,
,
∴![]() ,
,
∴M点的坐标为:![]() .
.
(2)∵A (0,5)、B (4,0)、C (2,5),
∴AO=5,AC=2,OB=4,
根据题意得,![]() ,
,
解得,![]() ,
,
∴![]() .
.
∴当![]() 时,重叠部分的面积比四边形BB′C′C的面积大.
时,重叠部分的面积比四边形BB′C′C的面积大.
(3)如图,由图形可得,阴影部分的面积等于梯形OBDO的面积,
过C作CM⊥x轴于M点,作DN⊥x轴于N点,
∴∠OND=∠NDO=∠OON=90°,
∴四边形ONDO是矩形,∴ON=OD,OO=ND=2
∵∠AOM=∠OMC=∠OAC=90°,
∴四边形OMCA是矩形,
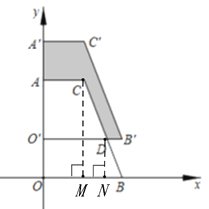
∴CM=OA=5,AC=OM=2
∴BM=OB-OM=4-2=2,
在Rt△CMB中,由勾股定理得BC=![]() ,
,
∵AC∥OD∥OB,
∴![]() ,
,
∴![]() ,
,
∴BD=![]() ,
,
在Rt△DNB中,由勾股定理得,BN=![]() ,
,
∴ON=OB-BN=4-![]() =
=![]() ,
,
∴ON=OD=![]() ,
,
∴S梯形OBDO=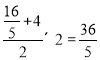 .
.
即阴影部分的面积为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,BE∥DF,∠DBE和∠CDF的角平分线交于点G.当∠BGD=65°时,∠BDC=________度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列单项式:
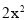 ,
,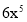 ,
,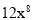 ,
,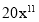 ,……按此规律写出第13个单项式是____.
,……按此规律写出第13个单项式是____. -
科目: 来源: 题型:
查看答案和解析>>【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m,宽为n)的盒子底部(如图②),盒子底部未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分周长和是_________(用代数式表示)

-
科目: 来源: 题型:
查看答案和解析>>【题目】济南某中学在参加“创文明城,点赞泉城”书画比赛中,杨老师从全校30个班中随机抽取了4个班(用A,B,C,D表示),对征集到的作鼎的数量进行了分析统计,制作了两幅不完整的统计图.
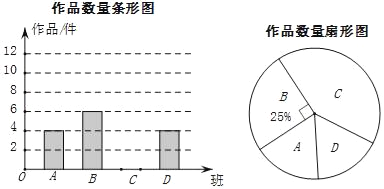
请根据以上信息,回答下列问题:
(l)杨老师采用的调查方式是 (填“普查”或“抽样调查”);
(2)请补充完整条形统计图,并计算扇形统计图中C班作品数量所对应的圆心角度数 .
(3)请估计全校共征集作品的什数.
(4)如果全枝征集的作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生,现要在获得一样等奖的作者中选取两人参加表彰座谈会,请你用列表或树状图的方法,求恰好选取的两名学生性别相同的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列各式:
 =
=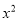 -1;
-1;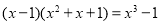 ;
;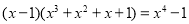 .
.(1)根据前面各式的规律可得:
①
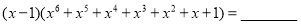 .
.②
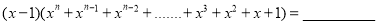 .
.(2)请用上面的结论进行计算:
①
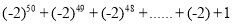 (答案可含有幂的形式表示);
(答案可含有幂的形式表示);②若
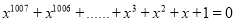 ,求
,求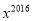 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列条件中不能确定四边形ABCD是平行四边形的是
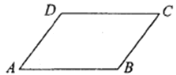
A.
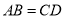 ,
, B.
B.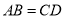 ,
,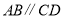
C.
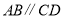 ,
, D.
D.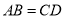 ,
,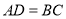
相关试题

