【题目】甲、乙两车同时同时出发从A地前往B地,乙行驶途中有一次停车修理,修好后乙车的行驶速度是原来的2倍.两车距离A地的路程![]() (千米)与行驶时间
(千米)与行驶时间![]() (时)的函数图象如图所示.
(时)的函数图象如图所示.

(1)求甲车距离A地的路程![]() (千米)与行驶时间
(千米)与行驶时间![]() (时)之间的函数关系式;
(时)之间的函数关系式;
(2)当x=2.8时,甲、乙两车之间的距离是 千米;乙车到达B地所用的时间![]() 的值为 ;
的值为 ;
(3)行驶过程中,两车出发多长时间首次后相遇?
参考答案:
【答案】(1)![]() ;(2)68,5.4;(3)4.5小时
;(2)68,5.4;(3)4.5小时
【解析】
试题(1)由题意设函数关系式为![]() ,根据待定系数法即可求得结果;
,根据待定系数法即可求得结果;
(2)把x=2.8代入(1)中的函数关系式即可得到甲车的路程,从而得到甲、乙两车之间的距离;先求出乙车开始的行驶速度,即可得到修好后乙车的行驶速度,从而得到a的值;
(3)设修好后乙车距离A地的路程![]() (千米)与行驶时间
(千米)与行驶时间![]() (时)的函数关系式为
(时)的函数关系式为![]() ,根据待定系数法求得函数关系式后,再与(1)中的函数关系式组成方程组求解即可.
,根据待定系数法求得函数关系式后,再与(1)中的函数关系式组成方程组求解即可.
(1)设函数关系式为![]()
∵图象过点(6,360)
∴![]() ,
,![]()
∴甲车距离A地的路程![]() (千米)与行驶时间
(千米)与行驶时间![]() (时)之间的函数关系式为
(时)之间的函数关系式为![]() ;
;
(2)在![]() 中,当x=2.8时,
中,当x=2.8时,![]() 千米;
千米;
则甲、乙两车之间的距离![]()
由图可得乙车开始的行驶速度为![]() 千米/时
千米/时
则修好后乙车的行驶速度为![]() 千米/时
千米/时
所以![]() ;
;
(3)设修好后乙车距离A地的路程![]() (千米)与行驶时间
(千米)与行驶时间![]() (时)的函数关系式为
(时)的函数关系式为![]()
∵图象过点(2.8,100),(5.4,360)
∴![]() ,解得
,解得![]()
∴函数关系式为![]()
由题意得![]() ,解得
,解得![]()
答:行驶过程中,两车出发4.5小时时间首次后相遇.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图,△ABC中,以AC为直径的⊙O与边AB交于点D,点E为⊙O上一点,连接CE并延长交AB于点F,连接ED.
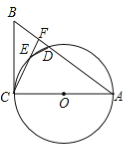
(1)若∠B+∠FED=90°,求证:BC是⊙O的切线;
(2)若FC=6,DE=3,FD=2,求⊙O的直径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
【1】求证:∠DAF=∠CDE
【2】问△ADF与△DEC相似吗?为什么?
【3】若AB=4,AD=3
 ,AE=3,求AF的长.
,AE=3,求AF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】《人民日报》2019年3月1日刊载了“2018年国民经济和社会发展统计公报”.有关脱贫攻坚的数据如下表.
年度
2014
2015
2016
2017
2018
农村贫困人口/万
7017
5575
4335
3046
1660
贫困发生率/%
7.2
5.7
4.5
3.1
1.7

(1)在给出图形中,直观表示近年农村贫困人口人数变化情况.
(2)根据你完善的统计图,写两点你获得的信息.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,点O是AC边上一点,连接BO交AD于F,OE⊥OB交BC边于点E.
(1)求证:△ABF∽△COE;
(2)当O为AC边中点,
 时,如图2,求
时,如图2,求 的值;
的值;(3)当O为AC边中点,
 时,请直接写出
时,请直接写出 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某织布厂有150名工人,为了提高经济效益,增设制衣项目,已知每人每天能织布30m,或利用所织布制衣4件,制衣一件需要布1.5m,将布直接出售,每米布可获利2元,将布制成衣后出售,每件可获利25元,若每名工人每天只能做一项工作,且不计其他因素,设安排x名工人制衣.
(1)一天中制衣所获利润P是多少(用含x的式子表示);
(2)一天中剩余布所获利润Q是多少 (用含x的式子表示);.
(3)一天当中安排多少名工人制衣时,所获利润为11806元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移6个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C2,使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.

相关试题

