Question

【题目】（10分）如图，△ABC中，以AC为直径的⊙O与边AB交于点D，点E为⊙O上一点，连接CE并延长交AB于点F，连接ED．

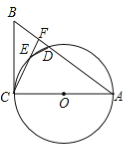
（1）若∠B+∠FED=90°，求证：BC是⊙O的切线；

（2）若FC=6，DE=3，FD=2，求⊙O的直径．

Answer 1

【答案】(1)详见解析；（2）⊙O的直径为9．

【解析】

试题分析： （1）由圆内接四边形对角互补可得∠A+∠DEC=180°，由邻补角的定义可得∠FED+∠DEC=180°，所以∠FED=∠A，又因∠B+∠FED=90°，即可得∠B+∠A=90°，所以∠BCA=90°，即BC是⊙O的切线；（2）由∠CFA=∠DFE，∠FED=∠A，即可得△FED∽△FAC，根据相似三角形的性质可得，带入数值即可求出AC的长．

试题解析：（1）证明：∵∠A+∠DEC=180°，∠FED+∠DEC=180°，

∴∠FED=∠A，

∵∠B+∠FED=90°，

∴∠B+∠A=90°，

∴∠BCA=90°，

∴BC是⊙O的切线；

（2）解：∵∠CFA=∠DFE，∠FED=∠A，

∴△FED∽△FAC，

∴，

∴，

解得：AC=9，即⊙O的直径为9．