【题目】如图,已知抛物线y=ax2﹣2ax﹣3a(a<0)与x轴交于A,B两点,点A在点B的左边,与y轴交于点C,顶点为D,若以BD为直径的⊙M经过点C.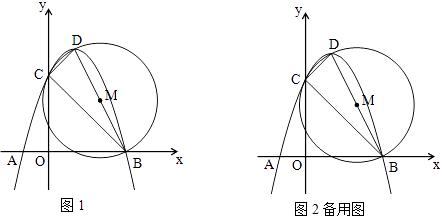
(1)请直接写出C,D两点的坐标(用含a的代数式表示);
(2)求抛物线的函数表达式;
(3)在抛物线上是否存在点E,使∠EDB=∠CBD?若存在,请求出所有满足条件的点E的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:∵将x=0代入抛物线的解析式得y=﹣3a,
∴点C的坐标是(0,﹣3a).
∵x=﹣ ![]() =
= ![]() =1,
=1,
∴点D的横坐标为1.
∵将x=1代入抛物线的解析式得y=a﹣2a﹣3a=﹣4a,
∴点D的坐标是(1,﹣4a).
(2)
解:解:令y=0得:ax2﹣2ax﹣3a=0
∵a≠0,故得x1=﹣1,x2=3
∴A(﹣1,0),B(3,0).
如图1所示:过点D作DN⊥y轴于点N,则DN=1,CN=﹣4a﹣(﹣3a)=﹣a.
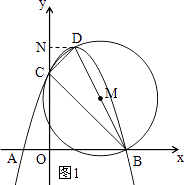
∵BD为⊙M的直径,
∴∠BCD=90°.
∴∠DCN+∠BCO=90°.
∵∠CDN+∠DCN=90°,
∴∠BCO=∠CDN,
∵∠BOC=∠DNC=90°,
∴△BOC∽△CND.
∴ ![]() ,即
,即 ![]() ,解得:a=±1(其中a=1舍去),
,解得:a=±1(其中a=1舍去),
∴a=﹣1.
∴所求抛物线为y=﹣x2+2x+3.
(3)
解:∵a=﹣1,
∴D(1,4).
∵设直线BC的解析式为y=kx+b,将B(3,0),C(0,3)代入得: ![]() ,解得:k=﹣1,b=3,
,解得:k=﹣1,b=3,
∴直线BC为:y=﹣x+3.
如图2所示:过点D作DE∥BC,交抛物线与点E.
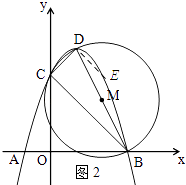
∵DE∥BC,
∴∠EDB=∠CBD.
∴设直线DE为y=﹣x+b
∵把点D(1,4)代入得:4=﹣1+b,解得:b=5,
∴直线DE为:y=﹣x+5.
解方程组 ![]() 得:
得: ![]() ,
, ![]()
∵D(1,4)
∴E(2,3).
如图3所示:作∠PDB=∠CBD,DP交BC于点P,交抛物线与点E.
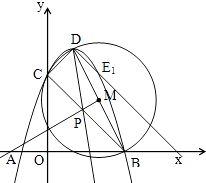
∵∠EDB=∠CBD,
∴PD=PB.
又∵MB=MD,
∴PM⊥BD.
∵B(3,0),D(1,4),
∴直线BD为y=﹣2x+6,且M(2,2)
∴设直线PM为 ![]() ,
,
∴2=1+b2,
∴b2=1
∴直线PM为: ![]()
解方程组 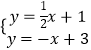 得:
得: ![]() ,
,
∴P( ![]() ,
, ![]() )
)
∵D(1,4),P( ![]() ,
, ![]() )
)
∴直线PD为:y=﹣7x+11
解方程组 ![]() 得:
得: ![]() ,
, ![]()
∵D(1,4),
∴E(8,﹣45).
综上所述,在抛物线上存在满足条件的点E,点E的坐标为E(2,3)或E(8,﹣45).
【解析】(1)将x=0代入抛物线的解析式可得到点C的坐标,依据抛物线的对称轴方程可求得点D的横坐标,然后将点D的横坐标代入可求得点D的纵坐标;(2)令y=0可求得点A、B的坐标,过点D作DN⊥y轴于点N,则DN=1,CN=﹣a.接下来证明△BOC∽△CND,然后依据相似三角形的性质可求得a的值,从而得到抛物线的解析式;(3)先求得点D的坐标、直线BC的解析式,点D作DE∥BC,交抛物线与点E.设直线DE的解析式为y=﹣x+b,把点D(1,4)代入直线DE的解析式求得b的值,然后将DE的解析式与抛物线的解析式组成方程可求得点E的坐标;作∠PDB=∠CBD,DP交BC于点P,交抛物线与点E.克证明MP垂直平分BD,从而可求得PM的解析式,然后由PM的解析式和BC的解析式可求得点P的坐标,接下来求得PD的解析式,最后根据DP的解析式和抛物线的解析式可求得E的坐标.
【考点精析】掌握二次函数的概念和二次函数的图象是解答本题的根本,需要知道一般地,自变量x和因变量y之间存在如下关系:一般式:y=ax2+bx+c(a≠0,a、b、c为常数),则称y为x的二次函数;二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为丰富学生的校园生活,准备从友谊体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同、每个篮球的价格相同),若购买3个篮球和2个足球共需420元;购买2个篮球和4个足球共需440元.
(1)购买一个篮球、一个足球各需多少元?
(2)根据该中学的实际情况,需要从该体育用品商店一次性购买足球和篮球共20个.要求购买篮球数不少于足球数的2倍,总费用不超过1840元,那么这所中学有哪几种购买方案?哪种方案所需费用最少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形OABC中,OA=3,AB=6,以OA,OC所在的直线为坐标轴,建立如图1的平面直角坐标系.将矩形OABC绕点O顺时针方向旋转,得到矩形ODEF,当点B在直线DE上时,设直线DE和x轴交于点P,与y轴交于点Q.
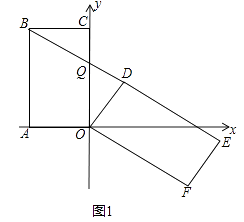
(1)求证:△BCQ≌△ODQ;
(2)求点P的坐标;
(3)若将矩形OABC向右平移(图2),得到矩形ABCG,设矩形ABCG与矩形ODEF重叠部分的面积为S,OG=x,请直接写出x≤3时,S与x之间的函数关系式,并且写出自变量x的取值范围.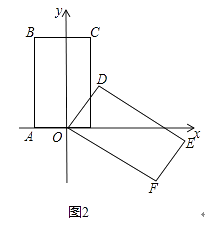
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下是某网络书店
 月关于图书销售情况的两个统计图:
月关于图书销售情况的两个统计图:
(
 )求
)求 月份该网络书店绘本类图书的销售额.
月份该网络书店绘本类图书的销售额.(
 )若已知
)若已知 月份与
月份与 月份这两个月的绘本类图书销售额相同,请补全统计图
月份这两个月的绘本类图书销售额相同,请补全统计图 .
.(
 )有以下两个结论:
)有以下两个结论:①该书店第一季度的销售总额为
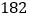 万元.
万元.②该书店
 月份到
月份到 月份绘本类图书销售额的月增长率相等.
月份绘本类图书销售额的月增长率相等.请你判断以上两个结论是否正确,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】通过对某校营养午餐的检测,得到如下信息:每份营养午餐的总质量
 ;午餐的成分
;午餐的成分为蛋白质、碳水化合物、脂肪和矿物质,其组成成分所占比例如图
 所示;其中矿物质的含量是脂
所示;其中矿物质的含量是脂肪含量的
 倍,蛋白质和碳水化合物含量占
倍,蛋白质和碳水化合物含量占 .
.
(
 )设其中蛋白质含量是
)设其中蛋白质含量是 .脂肪含量是
.脂肪含量是 ,请用含
,请用含 或
或 的代数式分别表示碳水化合物和矿物
的代数式分别表示碳水化合物和矿物质的质量.
(
 )求每份营养午餐中蛋白质、碳水化合物、脂肪和矿物质的质量.
)求每份营养午餐中蛋白质、碳水化合物、脂肪和矿物质的质量.(
 )参考图
)参考图 ,请在图
,请在图 中完成这四种不同成分所占百分比的扇形统计图.
中完成这四种不同成分所占百分比的扇形统计图. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知A(0,a)、B(b, 0),且a、b满足:
 ,点D为x正半轴上一动点
,点D为x正半轴上一动点 (1)求A、B两点的坐标
(2)如图,∠ADO的平分线交y轴于点C,点 F为线段OD上一动点,过点F作CD的平行线交y轴于点H,且∠AFH=45°, 判断线段AH、FD、AD三者的数量关系,并予以证明

(3)以AO为腰,A为顶角顶点作等腰△ADO,若∠DBA=30°,直接写出∠DAO的度数

-
科目: 来源: 题型:
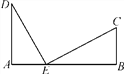
查看答案和解析>>【题目】如图,铁路上A,B两点相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15 km,CB=10 km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少千米处?
相关试题

