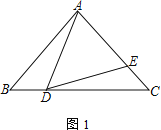
【题目】已知:△ABC中,点D为边BC上一点,点E在边AC上,且∠ADE=∠B
(1) 如图1,若AB=AC,求证:![]() ;
;
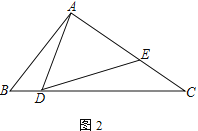
(2) 如图2,若AD=AE,求证:![]() ;
;
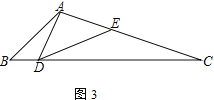
(3) 在(2)的条件下,若∠DAC=90°,且CE=4,tan∠BAD=![]() ,则AB=____________.
,则AB=____________.
参考答案:
【答案】![]()
【解析】分析:(1)![]()
![]()
∠ADE=∠B,可得![]()
![]() 根据等边对等角得到
根据等边对等角得到![]()
△BAD∽△CDE,根据相似三角形的性质即可证明.
(2) 在线段AB上截取DB=DF,证明△AFD∽△DEC,根据相似三角形的性质即可证明.
(3) 过点E作EF⊥BC于F,根据tan∠BAD=tan∠EDF=![]() ,设EF=x,DF=2x,则DE=
,设EF=x,DF=2x,则DE=![]() ,证明△EDC∽△GEC,求得
,证明△EDC∽△GEC,求得![]() ,根据CE2=CD·CG,求出CD=
,根据CE2=CD·CG,求出CD=![]() ,
,
根据△BAD∽△GDE,即可求出![]() 的长度.
的长度.
详解:(1) ![]()
![]()
∠ADE=∠B,可得![]()
![]()
![]()
![]()
∵△BAD∽△CDE,
∴![]() ;
;
(2) 在线段AB上截取DB=DF
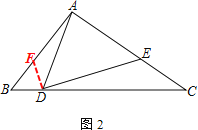
∴∠B=∠DFB=∠ADE
∵AD=AE ∴∠ADE=∠AED ∴∠AED=∠DFB,
同理:∵∠BAD+∠BDA=180°-∠B,∠BDA+∠CDE=180°-∠ADE
∴∠BAD=∠CDE
∵∠AFD=180°-∠DFB,∠DEC=180°-∠AED
∴∠AFD=∠DEC ,
∴△AFD∽△DEC,
∴![]()
(3) 过点E作EF⊥BC于F
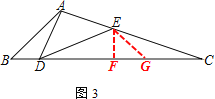
∵∠ADE=∠B=45°
∴∠BDA+∠BAD=135°,∠BDA+∠EDC=135°
∴∠BAD=∠EBC(三等角模型中,这个始终存在)
∵tan∠BAD=tan∠EDF=![]()
∴设EF=x,DF=2x,则DE=![]() ,
,
在DC上取一点G,使∠EGD=45°,
∴△BAD∽△GDE,
∵AD=AE∴∠AED=∠ADE=45°,
∵∠AED=∠EDC+∠C=45°,∠C+∠CEG=45°,∴∠EDC=∠GEC,
∴△EDC∽△GEC,∴![]() ∴
∴![]() ,
,![]()
又CE2=CD·CG,
∴42=CD·![]() ,CD=
,CD=![]() ,
,
∴![]() ,解得
,解得![]()
∵△BAD∽△GDE
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x1,x2是一元二次方程(a﹣6)x2+2ax+a=0的两个实数根.
(1)是否存在实数a,使﹣x1+x1x2=4+x2成立?若存在,求出a的值;若不存在,请你说明理由;
(2)求使(x1+1)(x2+1)为正整数的实数a的整数值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】哈尔滨地铁“二号线”正在进行修建,现有大量的残土需要运输.某车队有载重量为8吨、10吨的卡车共12台,全部车辆运输一次可以运输110吨残土.
(1)求该车队有载重量8吨、10吨的卡车各多少辆?
(2)随着工程的进展,该车队需要一次运输残土不低于165吨,为了完成任务,该车队准备再新购进这两种卡车共6辆,则最多购进载重量为8吨的卡车多少辆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,锐角△ABC的两条高CD、BE相交于点O,且OB=OC
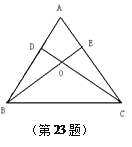
1.求证:△ABC是等腰三角形
2.连结AO,判断AO与BC的位置关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了改善办学条件,计划购置一批电子白板和一批笔记本电脑,经投标,购买1块电子白板比买3台笔记本电脑多3000元,购买4块电子白板和5台笔记本电脑共需80000元.
(1)求购买1块电子白板和一台笔记本电脑各需多少元?
(2)根据该校实际情况,需购买电子白板和笔记本电脑的总数为396,要求购买的总费用不超过2700000元,并购买笔记本电脑的台数不超过购买电子白板数量的3倍,该校有哪几种购买方案?
(3)上面的哪种购买方案最省钱?按最省钱方案购买需要多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;
(2)平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2 ;
(3)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
相关试题

