【题目】已知:如图,锐角△ABC的两条高CD、BE相交于点O,且OB=OC
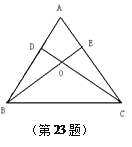
1.求证:△ABC是等腰三角形
2.连结AO,判断AO与BC的位置关系,并说明理由.
参考答案:
【答案】1.见解析;2.AO⊥BC
【解析】
(1)由OB=OC得到∠OBC=∠OCB,在△BCD与△BEC中利用内角和定理以及等量代换即得到∠ABC=∠ACB,故△ABC为等腰三角形
(2)连接AO并延长交BC于F,易证△AOB≌△AOC,得到AF为∠BAC的角平分线,得到OA⊥BC
(1)∵OB=OC,
∴∠OBC=∠OCB,
∵锐角△ABC的两条高BD、CE相交于点O,
∴∠BEC=∠BDC=90°,
∵∠BEC+∠BCE+∠ABC=∠BDC+∠DBC+∠ACB=180°,
∴∠ABC=∠ACB,
∴AB=AC,
∴△ABC是等腰三角形;
(2)AO⊥BC
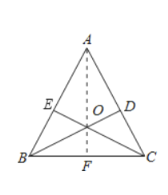
理由:连接AO并延长交BC于F,
∵AB=AC,OB=OC,
又∵OA=OA,
∴△AOB≌△AOC.
∴∠BAF=∠CAF,
∴AF为∠BAC的角平分线
又∵△ABC为等腰三角形
∴OA⊥BC
-
科目: 来源: 题型:
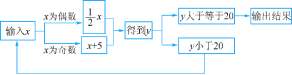
查看答案和解析>>【题目】按如图所示的程序计算,若输入的值x=17,则输出的结果为22;若输入的值x=34,则输出的结果为22.当输出的值为24时,则输入的x的值在0至40之间的所有正整数是____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x1,x2是一元二次方程(a﹣6)x2+2ax+a=0的两个实数根.
(1)是否存在实数a,使﹣x1+x1x2=4+x2成立?若存在,求出a的值;若不存在,请你说明理由;
(2)求使(x1+1)(x2+1)为正整数的实数a的整数值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】哈尔滨地铁“二号线”正在进行修建,现有大量的残土需要运输.某车队有载重量为8吨、10吨的卡车共12台,全部车辆运输一次可以运输110吨残土.
(1)求该车队有载重量8吨、10吨的卡车各多少辆?
(2)随着工程的进展,该车队需要一次运输残土不低于165吨,为了完成任务,该车队准备再新购进这两种卡车共6辆,则最多购进载重量为8吨的卡车多少辆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC中,点D为边BC上一点,点E在边AC上,且∠ADE=∠B
(1) 如图1,若AB=AC,求证:
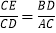 ;
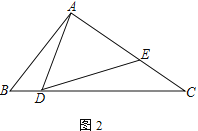
;(2) 如图2,若AD=AE,求证:
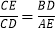 ;
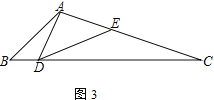
;(3) 在(2)的条件下,若∠DAC=90°,且CE=4,tan∠BAD=
 ,则AB=____________.
,则AB=____________. 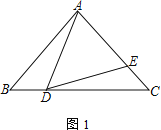
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了改善办学条件,计划购置一批电子白板和一批笔记本电脑,经投标,购买1块电子白板比买3台笔记本电脑多3000元,购买4块电子白板和5台笔记本电脑共需80000元.
(1)求购买1块电子白板和一台笔记本电脑各需多少元?
(2)根据该校实际情况,需购买电子白板和笔记本电脑的总数为396,要求购买的总费用不超过2700000元,并购买笔记本电脑的台数不超过购买电子白板数量的3倍,该校有哪几种购买方案?
(3)上面的哪种购买方案最省钱?按最省钱方案购买需要多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;
(2)平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2 ;
(3)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标 .

相关试题

