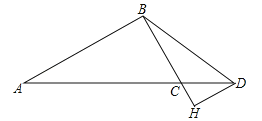
【题目】如图,在△ABC中,∠ABC=90°,BC=3,D为AC延长线上一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H.
(1)求BDcos∠HBD的值;
(2)若∠CBD=∠A,求AB的长.
参考答案:
【答案】(1)4;(2)6.
【解析】
试题分析:(1)首先根据DH∥AB,判断出△ABC∽△DHC,即可判断出![]() =3;然后求出BH的值是多少,再根据在Rt△BHD中,cos∠HBD=
=3;然后求出BH的值是多少,再根据在Rt△BHD中,cos∠HBD=![]() ,求出BDcos∠HBD的值是多少即可;
,求出BDcos∠HBD的值是多少即可;
(2)首先判断出△ABC∽△BHD,推得![]() ;然后根据△ABC∽△DHC,推得
;然后根据△ABC∽△DHC,推得![]() ,所以AB=3DH;最后根据
,所以AB=3DH;最后根据![]() ,求出DH的值是多少,进而求出AB的值是多少即可.
,求出DH的值是多少,进而求出AB的值是多少即可.
试题解析:(1)∵DH∥AB,∴∠BHD=∠ABC=90°,∴△ABC∽△DHC,∴![]() =3,∴CH=1,BH=BC+CH,在Rt△BHD中,cos∠HBD=
=3,∴CH=1,BH=BC+CH,在Rt△BHD中,cos∠HBD=![]() ,∴BDcos∠HBD=BH=4;
,∴BDcos∠HBD=BH=4;
(2)∵∠CBD=∠A,∠ABC=∠BHD,∴△ABC∽△BHD,∴![]() ,∵△ABC∽△DHC,∴
,∵△ABC∽△DHC,∴![]() ,∴AB=3DH,∴
,∴AB=3DH,∴![]() ,解得DH=2,∴AB=3DH=3×2=6,即AB的长是6.
,解得DH=2,∴AB=3DH=3×2=6,即AB的长是6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.﹣a2?(﹣a3)=a6
B.(a2)﹣3=a﹣6
C.( )﹣2=﹣a2﹣2a﹣1
)﹣2=﹣a2﹣2a﹣1
D.(2a+1)0=1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图等边△ABC边长为1cm,D、E分别是AB、AC上两点,将△ADE沿直线DE折叠,点A落在A’处,A在△ABC外,则阴影部分图形周长为( )
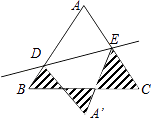
A.1cm
B.1.5cm
C.2cm
D.3cm -
科目: 来源: 题型:
查看答案和解析>>【题目】问题情景:如图1,AB∥CD,∠PAB=140°,∠PCD=135°,求∠APC的度数.
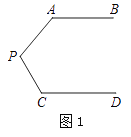
(1)丽丽同学看过图形后立即口答出:∠APC=85°,请你补全她的推理依据.
如图2,过点P作PE∥AB,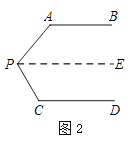
∵AB∥CD,∴PE∥CD. ()
∴∠A+∠APE=180°.
∠C+∠CPE=180°. ()
∵∠PAB=140°,∠PCD=135°,
∴∠APE=40°,∠CPE=45°
∴∠APC=∠APE+∠CPE=85°.()
问题迁移:
(2)如图3,AD∥BC,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β,求∠CPD与∠α、∠β之间有何数量关系?请说明理由.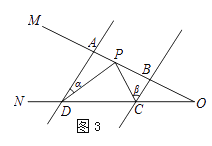
(3)在(2)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD与∠α、∠β之间的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中正确的是( )
A. 两条对角线互相平分的四边形是平行四边形
B. 两条对角线相等的四边形是矩形
C. 两条对角线互相垂直的四边形是菱形
D. 两条对角线互相垂直且平分的四边形是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知:∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
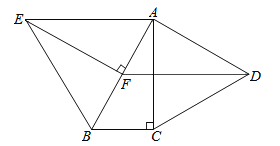
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中,计算正确的是( )
A.(15x2y﹣5xy2)÷5xy=3x﹣5y
B.98×102=(100﹣2)(100+2)=9996
C.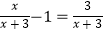
D.(3x+1)(x﹣2)=3x2+x﹣2
相关试题

