【题目】已知A(2,-3)、P(3,![]() )、Q(-5,b)都在反比例函数的图象y=
)、Q(-5,b)都在反比例函数的图象y=![]() (k≠0)上.
(k≠0)上.
(1)求此反比例函数解析式;
(2)求a+![]() 的值;
的值;
(3)若反比例函数y=![]() 经过A′(2,3),点P和点Q关于y轴的对称点P′、Q′在反比例函数y=
经过A′(2,3),点P和点Q关于y轴的对称点P′、Q′在反比例函数y=![]() 的图象上吗?通过计算说明理由.
的图象上吗?通过计算说明理由.
参考答案:
【答案】(1) y=-![]() ;(2)-3;(3)点P和点Q关于y轴的对称点P′、Q′在y=
;(2)-3;(3)点P和点Q关于y轴的对称点P′、Q′在y=![]() 的图象上.
的图象上.
【解析】试题分析:![]() 将A(2,-3)代入反比例函数
将A(2,-3)代入反比例函数![]() ,求出
,求出![]() 的值即可.
的值即可.
![]() 将点
将点![]() 代入
代入![]() ,求得
,求得![]() 的值,代入运算即可.
的值,代入运算即可.
![]() 求出点
求出点![]() 关于
关于![]() 轴的对称点,代入验证即可.
轴的对称点,代入验证即可.
试题解析:(1)∵将A(2,-3)代入反比例函数![]() ,得
,得![]()
解得,k=6.
∴反比例函数表达式为:![]()
![]() 将点
将点![]() 代入
代入![]() ,
,
即![]()
解得:![]()
![]()
![]() 若反比例函数
若反比例函数![]() 经过
经过![]() 则反比例函数的解析式为
则反比例函数的解析式为![]()
点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 都在反比例函数
都在反比例函数![]() 的图象上.
的图象上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l为正比例函数y=x的图象,点A1的坐标为(1,0),过点A1作x轴的垂线交直线l于点D1,以A1D1为边作正方形A1B1C1D1;过点C1作直线l的垂线,垂足为A2,交x轴于点B2,以A2B2为边作正方形A2B2C2D2;过点C2作x轴的垂线,垂足为A3,交直线l于点D3,以A3D3为边作正方形A3B3C3D3,…,按此规律操作下所得到的正方形AnBnCnDn的面积是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的曲线是函数y=
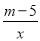 (m为常数)图象的一支.
(m为常数)图象的一支.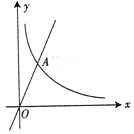
(1)求常数m的取值范围;
(2)若该函数的图象与正比例函数y=2x的图象在第一象限的交点为A(2,n),求点A的坐标及反比例
函数的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了庆祝校园艺术节,准备购买一批盆花布置校园.已知1盆A种花和2盆B种花一共需13元,2盆A种花和1盆B种花一共需11元.
(1)求1盆A种花和1盒B种花的售价各是多少元?
(2)学校准备购进这两种盆花共100盆,并且A种盆花的数量不超过B种盆花数量的2倍,请求出A种盆花的数量最多是多少?
-
科目: 来源: 题型:
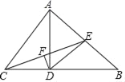
查看答案和解析>>【题目】如图,AD是△ABC的高,CE是△ABC的中线.
(1)若AD=12,BD=16,求DE;
(2)已知点F是中线CE的中点,连接DF,若∠AEC=57°,∠DFE=90°,求∠BCE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司欲招聘一名部门经理,对甲、乙、丙三名候选人进行了三项素质测试.各项测试成绩如表格所示:
测试项目
测试成绩
甲
乙
丙
专业知识
74
87
90
语言能力
58
74
70
综合素质
87
43
50
(1)如果根据三次测试的平均成绩确定人选,那么谁将被录用?
(2)根据实际需要,公司将专业知识、语言能力和综合素质三项测试得分按4:3:1的比例确定每个人的测试总成绩,此时谁将被录用?
(3)请重新设计专业知识、语言能力和综合素质三项测试得分的比例来确定每个人的测试总成绩,使得乙被录用,若重新设计的比例为x:y:1,且x+y+1=10,则x= ,y= .(写出x与y的一组整数值即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形OABC中,O为平面直角坐标系的原点,点A的坐标为(a,0),点C的坐标为(0,b)且a、b满足
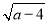 +|b﹣6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的线路移动.
+|b﹣6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的线路移动.(1)点B的坐标为 ;当点P移动3.5秒时,点P的坐标为 ;
(2)在移动过程中,当点P到x轴的距离为4个单位长度时,求点P移动的时间;
(3)在O﹣C﹣B的线路移动过程中,是否存在点P使△OBP的面积是10,若存在求出点P移动的时间;若不存在,请说明理由.
相关试题

