【题目】已知方程x+![]() (c是常数,c≠0)的解是c或
(c是常数,c≠0)的解是c或![]() ,那么方程x+
,那么方程x+![]() (a是常数,且a≠0)的解是_____或_____.
(a是常数,且a≠0)的解是_____或_____.
参考答案:
【答案】 ![]()
![]()
【解析】分析:观察方程x+![]() (c是常数,c≠0)的特点,发现此方程的左边是未
(c是常数,c≠0)的特点,发现此方程的左边是未
知数与其倒数的和,方程右边的形式与左边的形式完全相同,只是把其中的未知数换成了某
个常数,那么这样的方程可以直接求解.本题需要将方程x+![]() 变形,使等号
变形,使等号
左边未知数的系数变得相同,又等号右边的代数式可变为![]() .为此,方程的两边
.为此,方程的两边
同乘2,整理后,即可写成方程 x+![]() 的形式,从而求出原方程的解.
的形式,从而求出原方程的解.
详解:原方程变形为![]() =
=![]() +
+![]() +
+![]() ,
,
方程的两边同乘2,得2x+![]() =a+3+
=a+3+![]() ,
,
两边同时减去3,得2x﹣3+![]() =a+
=a+![]() ,
,
∴2x﹣3=a或2x﹣3=![]() ,
,
∴x=![]() 或x=
或x=![]() .
.
故答案为![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在ABCD中,E是AD边的中点,连接BE.
(1)如图①,若BC=2,则AE的长=__;
(2)如图②,延长BE交CD的延长线于点F,求证:FD=AB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】求1+2+22+23…+22012的值,可令S=1+2+22+23+…+22012,则2S=2+22+23+24+…+22013,因此2S﹣S=22013﹣1,仿照以上推理,计算出1+5+52+53+…+52017的值为( )
A. 52017﹣1 B. 52018﹣1 C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD,过D作BD的垂线,与BC延长线交于E点,F为BE的中点,连接DF,已知DF=4,设AB=x,AD=y,求代数式x2+(y﹣4)2的值.

-
科目: 来源: 题型:
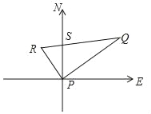
查看答案和解析>>【题目】如图,某港口P位于东西方向的海岸线上,A、B两艘轮船同时从港口P出发,各自沿一固定方向航行,A轮船每小时航行12海里,B轮船每小时航行16海里.它们离开港口一个半小时后分别位于点R、Q处,且相距30海里.已知B轮船沿北偏东60°方向航行.
(1)A轮船沿哪个方向航行?请说明理由;
(2)请求出此时A轮船到海岸线的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=BD,点E,F分别在BC,CD边上,且CE=DF,BF与DE交于点G,若BG=2,DG=4,则CD长为__.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A的坐标为(﹣
 ,0),点B的坐标为(0,3).
,0),点B的坐标为(0,3).(1)求过A,B两点直线的函数表达式;
(2)过B点作直线BP与x轴交于点P,且使OP=2OA,求△ABP的面积.

相关试题

