【题目】如图,正五边形的边长为2,连对角线AD,BE,CE,线段AD分别与BE和CE相交于点M,N,则MN=__________;

参考答案:
【答案】3-![]()
【解析】根据正五边形的性质得到∠ABE=∠AEB=∠EAD=36°,根据三角形的内角和即可得到结论;由于∠AEN=108°﹣36°=72°,∠ANE=36°+36°=72°,得到∠AEN=∠ANE,根据等腰三角形的判定定理得到AE=AN,同理DE=DM,根据相似三角形的性质得到![]() ,等量代换得到AN2=AMAD;根据AE2=AMAD,列方程得到MN=3﹣
,等量代换得到AN2=AMAD;根据AE2=AMAD,列方程得到MN=3﹣![]() ;
;
解:∵∠BAE=∠AED=108°,
∵AB=AE=DE,
∴∠ABE=∠AEB=∠EAD=36°,
∴∠AME=180°﹣∠EAM﹣∠AEM=108°,
∵∠AEN=108°﹣36°=72°,∠ANE=36°+36°=72°,
∴∠AEN=∠ANE,
∴AE=AN,
同理DE=DM,
∴AE=DM,
∵∠EAD=∠AEM=∠ADE=36°,
∴△AEM∽△ADE,
∴![]() ,
,
∴AE2=AMAD;
∴AN2=AMAD;
∵AE2=AMAD,
∴22=(2﹣MN)(4﹣MN),
∴MN=3﹣![]() .
.
“点睛”此题主要考查了正多边形的性质和相似三角形的性质,根据三角形的内角和、相似三角形的性质即可得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题:
①两点确定一条直线;②两点之间,线段最短;③对顶角相等;④内错角相等;
其中真命题的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,B是线段AD上一动点,沿A→D→A以2cm/s的速度往返运动1次,C是线段BD的中点,AD=10cm,设点B运动时间为t秒(0≤t≤10).

(1)当t=2时,①AB= ___ cm.②求线段CD的长度.
(2)用含t的代数式表示运动过程中AB的长.
(3)在运动过程中,若AB中点为E,则EC的长是否变化?若不变,求出EC的长;若发生变化,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若3x2﹣5x+1=0,则5x(3x﹣2)﹣(3x+1)(3x﹣1)=( )
A.﹣1B.0C.1D.﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据题意解答
(1)先化简,再求代数式的值:(1﹣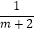 )÷
)÷ 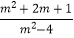 ,其中m=1.
,其中m=1.
(2)解方程: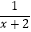 +
+  =0.
=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,正确的是( )
A.3a﹣2a=a
B.(a2)3=a5
C.a2a3=a6
D.a10÷a5=a2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果x=2是方程2x=5﹣a的解,那么a的值为( )
A. 2B. 6C. 1D. 12
相关试题

