【题目】如图,在四边形ABCD中,AC⊥CD于点C,BD平分∠ADC交AC于点E,∠1=∠2.
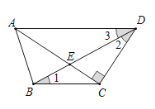
(1) 请完成下面的说理过程.
∵BD平分∠ADC(已知)
∴ (角平分线的定义)
∵∠1=∠2(已知)
∴
∴AD∥BC( )
(2)若∠BCE=20°,求∠1的度数.
参考答案:
【答案】(1)∠2=∠3,∠1=∠3,内错角相等,两直线平行;(2)35°
【解析】
(1)根据角平分线的定义,及平行线的判定定理即可求证;
(2)根据平行线的性质定理,可得∠ADC+∠BCD=180°,求得∠ADC度数,由(1)得∠1=∠2=∠3,即可求得∠1度数.
(1)∵BD平分∠ADC(已知)
∴∠2=∠3(角平分线的定义)
∵∠1=∠2(已知)
∴∠1=∠3
∴AD∥BC(内错角相等,两直线平行)
故答案为:∠2=∠3,∠1=∠3,内错角相等,两直线平行
(2)∵AC⊥CD
∴∠ACD=90°
∵∠BCE=20°
∴∠BCD=20°+90°=110°
∵AD∥BC
∴∠ADC+∠BCD=180°
∴∠ADC=180°-110°=70°
∵∠1=∠2=∠3=35°
故答案为:35°
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一商场计划到厂家购买电视机,已知该厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1100元,乙种每台1300元,丙种每台2100元.
(1)若商场同时购进其中两种不同型号的电视机共60台,用去7万元,请你帮助商场设计进货方案.
(2)若商场同时购进三种不同型号的电视机共50台,用去6万元,请你帮助商场设计进货方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法正确的个数是( )
①a>0;②b>0;③c<0;④b2﹣4ac>0;⑤a+b+c=0.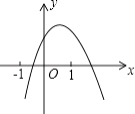
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点C为两条相互平行的直线AB,ED之间一点,
 和
和 的角平分线相交于F,若∠BCD=
的角平分线相交于F,若∠BCD= ∠BFD+10°,则
∠BFD+10°,则 的度数为__________.
的度数为__________.
-
科目: 来源: 题型:
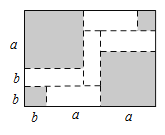
查看答案和解析>>【题目】如图,将一张大长方形纸板按图中虚线裁剪成9块,其中有2块是边长为a厘米的大正方形,2块是边长都为b厘米的小正方形,5块是长为a厘米,宽为b厘米的相同的小长方形,且a>b.
(1)观察图形,可以发现代数式2a+5ab+2b可以因式分解为 .
(2)若图中阴影部分的面积为242平方厘米,大长方形纸板的周长为78厘米,求图中空白部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,⊙P经过点A(0,
 )、O(0,0)、B(1,0),点C在第一象限的
)、O(0,0)、B(1,0),点C在第一象限的  上,则∠BCO的度数为 .
上,则∠BCO的度数为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角形坐标系中有两点A(6,0)、B(0,8),点C为AB的中点,点D在x轴上,当点D的坐标为时,由点A、C、D组成的三角形与△AOB相似.

相关试题

