Question

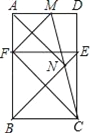
【题目】已知：矩形ABCD内一点N，△ANB为等腰直角三角形，连结BN、CN并延长分别交DC，AD于点E，M，在AB上截取BF=EC，连接MF．

（1）求证：四边形FBCE为正方形；

（2）求证：MN=NC；

（3）若S△FMC：S正方形FBCE=2：3，求BN：MD的值．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）BN：MD=．

【解析】试题分析：（1）先证明四边形为矩形，再利用为等腰直角三角形，证明为等腰直角三角形，则，所以四边形为正方形；
（2）作辅助线，构建全等三角形，证明≌，得，再利用平行线分线段成比例定理可得 则
（3）设 表示出和S正方形FBCE，并根据S△FMC:S正方形FBCE=2:3,依次计算出的长，最后得结论．

试题解析：(1)如图1，∵四边形ABCD为矩形，

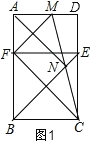
∴AB∥CD,

∴BF∥EC，

∵BF=EC，

∴四边形FBCE为矩形，

∵△ANB为等腰直角三角形，

∴△BEC为等腰直角三角形,

∴BC=CE，

∴四边形FBCE为正方形；

(2)如图2，过N作GH⊥BC，交BC于H，AD于G，则GH⊥AD，

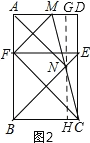
∴△BHN≌△AGN，

∴NG=NH，

∵AD∥BC，

∴

∴MN=NC；

(3)如图2,设BF=1,则S正方形FBCE=1,，

∵FO=OC，MN=NC，

∴ON∥FM，

由于S△FMC:S正方形FBCE=2:3,

即

∴△AFM是等腰直角三角形，