【题目】解下列方程
(1)![]() (用配方法) (2)
(用配方法) (2)![]()
(3)![]() (4)
(4)![]()
参考答案:
【答案】(1)![]() ,
, ![]() ;(2)x1=2,x2=3;(3)
;(2)x1=2,x2=3;(3)![]() ,
, ![]() ;
;
(4)![]() .
.
【解析】试题分析:
(1) 利用配方法解该方程时需要先将常数项移至等号右侧,再在方程两侧同时加上一次项系数一半的平方(这一步需要在二次项系数为1的前提下进行,本方程已自然满足),然后将方程整理为(x+m)2=n (m,n均为常数)的形式,利用直接开平方法求解.
(2) 观察方程两侧可知,方程两侧的整式具有公因式(x-2),故可以考虑将方程右侧的整式移至方程左侧并利用提公因式法对移项后的方程左侧进行因式分解,通过因式分解法解此一元二次方程.
(3) 观察方程形式可知,此方程需要用公式法进行求解. 先确定求根公式中各字母的具体数值,再计算![]() 的值. 若
的值. 若![]() 的值小于零,此方程无实数根;若
的值小于零,此方程无实数根;若![]() 的值大于等于零,则将各字母的值代入求根公式即可得解.
的值大于等于零,则将各字母的值代入求根公式即可得解.
(4) 将方程右侧的整式移至方程左侧,再对方程左侧用平方差公式进行因式分解,通过因式分解法解此一元二次方程.
试题解析:
(1) ![]()
移项,得 ![]() ,
,
方程两边同时加上一次项系数一半的平方,得 ![]() ,
,
整理,得 ![]() ,
,
直接开平方,得 ![]() ,
,
∴![]() ,
, ![]() .
.
(2) ![]()
移项,得 ![]() ,
,
方程左侧提公因式![]() ,得
,得 ![]() ,
,
整理并进一步进行因式分解,得 ![]() ,
,
∴![]() 或
或![]() ,
,
∴![]() ,
, ![]() .
.
(3) ![]()
∵a=2,b=![]() ,c=-5,
,c=-5,
∴![]()
∴ ,
,
∴![]() ,
, ![]()
(4) ![]()
移项,得 ![]() ,
,
方程左侧用平方差公式进行因式分解,得 ![]() ,
,
整理,得 ![]() ,
,
∴![]() 或
或![]() ,
,
∴![]() ,
, ![]() .
.
-
科目: 来源: 题型:
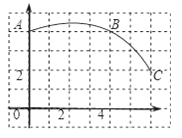
查看答案和解析>>【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1)请在图中确定该圆弧所在圆心D点的位置,D点坐标为 ;
(2)连接AD、CD,求⊙D的半径及扇形DAC的圆心角度数;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.
-
科目: 来源: 题型:
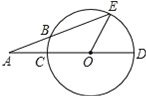
查看答案和解析>>【题目】已知,如图,CD为⊙O的直径,∠EOD=60°,AE交⊙O于点B,E,且AB=OC,求:(1)∠A的度数;(2)∠AEO度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:8(x+3)=3(x﹣2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.

(1)求证:AD⊥CD;
(2)若AD=2,AC=
 ,求AB的长.
,求AB的长. -
科目: 来源: 题型:
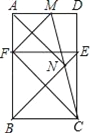
查看答案和解析>>【题目】已知:矩形ABCD内一点N,△ANB为等腰直角三角形,连结BN、CN并延长分别交DC,AD于点E,M,在AB上截取BF=EC,连接MF.
(1)求证:四边形FBCE为正方形;
(2)求证:MN=NC;
(3)若S△FMC:S正方形FBCE=2:3,求BN:MD的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个长为15m的梯子斜靠在墙上,梯子的顶端距地面的距离为12m,
①如果梯子的顶端下滑了1m,那么梯子的底端也向后滑动1m吗?请通过计算解答.
②梯子的顶端从A处沿墙AO下滑的距离与点B向外移动的距离有可能相等吗?若有可能,请求出这个距离,没有可能请说明理由.
③若将上题中的梯子换成15米长的直木棒,将木棒紧靠墙竖直放置然后开始下滑直至直木棒的顶端A滑至墙角O处,试求出木棒的中点Q滑动的路径长.

相关试题

