【题目】如图,点A1(2,2)在直线y=x上,过点A1作A1B1∥y轴交直线y= ![]() x于点B1 , 以点A1为直角顶点,A1B1为直角边在A1B1的右侧作等腰直角△A1B1C1 , 再过点C1作A2B2∥y轴,分别交直线y=x和y=
x于点B1 , 以点A1为直角顶点,A1B1为直角边在A1B1的右侧作等腰直角△A1B1C1 , 再过点C1作A2B2∥y轴,分别交直线y=x和y= ![]() x于A2 , B2两点,以点A2为直角顶点,A2B2为直角边在A2B2的右侧作等腰直角△A2B2C2…,按此规律进行下去,则等腰直角△AnBnCn的面积为(用含正整数n的代数式表示)
x于A2 , B2两点,以点A2为直角顶点,A2B2为直角边在A2B2的右侧作等腰直角△A2B2C2…,按此规律进行下去,则等腰直角△AnBnCn的面积为(用含正整数n的代数式表示) 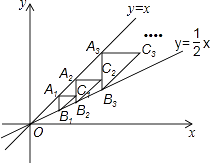
参考答案:
【答案】![]()
【解析】解:∵点A1(2,2),A1B1∥y轴交直线y= ![]() x于点B1 ,
x于点B1 ,
∴B1(2,1)
∴A1B1=2﹣1=1,即△A1B1C1面积= ![]() ×12=
×12= ![]() ;
;
∵A1C1=A1B1=1,
∴A2(3,3),
又∵A2B2∥y轴,交直线y= ![]() x于点B2 ,
x于点B2 ,
∴B2(3, ![]() ),
),
∴A2B2=3﹣ ![]() =
= ![]() ,即△A2B2C2面积=
,即△A2B2C2面积= ![]() ×(
×( ![]() )2=
)2= ![]() ;
;
以此类推,
A3B3= ![]() ,即△A3B3C3面积=
,即△A3B3C3面积= ![]() ×(
×( ![]() )2=
)2= ![]() ;
;
A4B4= ![]() ,即△A4B4C4面积=
,即△A4B4C4面积= ![]() ×(
×( ![]() )2=
)2= ![]() ;
;
…
∴AnBn=( ![]() )n﹣1 , 即△AnBnCn的面积=
)n﹣1 , 即△AnBnCn的面积= ![]() ×[(
×[( ![]() )n﹣1]2=
)n﹣1]2= ![]() .
.
故答案为: ![]()

先根据点A1的坐标以及A1B1∥y轴,求得B1的坐标,进而得到A1B1的长以及△A1B1C1面积,再根据A2的坐标以及A2B2∥y轴,求得B2的坐标,进而得到A2B2的长以及△A2B2C2面积,最后根据根据变换规律,求得AnBn的长,进而得出△AnBnCn的面积即可.本题主要考查了一次函数图象上点的坐标特征以及等腰直角三角形的性质,解决问题的关键是通过计算找出变换规律,根据AnBn的长,求得△AnBnCn的面积.解题时注意:直线上任意一点的坐标都满足函数关系式y=kx+b.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AD∥BC,AB=4cm,BC=8cm,动点M从点D出发,按折线DCBAD方向以2cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1cm/s的速度运动.
(1)若动点M、N同时出发,经过几秒钟两点相遇?
(2)若点E在线段BC上,且BE=3cm,若动点M、N同时出发,相遇时停止运动,经过几秒钟,点A、E、M、N组成平行四边形?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形OABC为矩形,点A,C分别在x轴和y轴上,连接AC,点B的坐标为(4,3),∠CAO的平分线与y轴相交于点D,则点D的坐标为 .
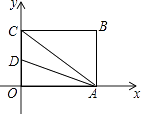
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△AOB中,∠AOB=90°,点A的坐标为(2,1),BO=2
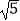 ,反比例函数y=
,反比例函数y= 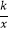 的图象经过点B,则k的值为 .
的图象经过点B,则k的值为 . 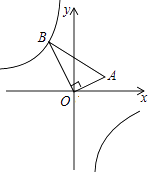
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是等边三角形ABC内的一点,且PA=3,PB=3,PC=5,以BC为边在△ABC外作△BQC≌△BPA,连接PQ,则以下结论错误的是()

A. △BPQ是等边三角形 B. △PCQ是直角三角形 C. ∠APB=150° D. ∠APC=135°
-
科目: 来源: 题型:
查看答案和解析>>【题目】台风是一种自然灾害,它以台风中心为圆心,在周围数十千米范围内形气旋风暴,有极强的破坏力,此时某台风中心在海域B处,在沿海城市A的正南方向240千米,其中心风力为12级,每远离台风中心25千米,台风就会减弱一级,如图所示,该台风中心正以20千米/时的速度沿北偏东30°方向向C移动,且台风中心的风力不变,若城市所受风力达到或超过4级,则称受台风影响. 试问:

(1)A城市是否会受到台风影响?请说明理由.
(2)若会受到台风影响,那么台风影响该城市的持续时间有多长?
(3)该城市受到台风影响的最大风力为几级?
-
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形的一边长为10,那么它的两条对角线的长度可以是( )。
A. 8和12 B. 4和20 C. 20和40 D. 8和6
相关试题

