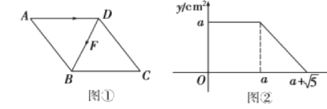
【题目】如图①,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B.图②是点F运动时,△FBC的面积y(cm![]() )随时间x(s)变化的关系图象,则a的值是__
)随时间x(s)变化的关系图象,则a的值是__
参考答案:
【答案】![]()
【解析】
过点D作DE⊥BC于点E,通过分析图象,点F从点A到D用a s,此时,△FBC的面积为a,依此可求菱形的高DE;再由图象可知,BD=![]() ,在Rt△DBE中应用勾股定理求BE的值,进而在Rt△DEC应用勾股定理求a的值.
,在Rt△DBE中应用勾股定理求BE的值,进而在Rt△DEC应用勾股定理求a的值.
过点D作DE⊥BC于点E.
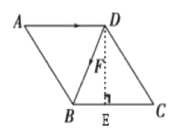
由图象可知,点F由点A到点D用时为a s,△FBC的面积为a cm![]() .
.
∴AD=a,
∴![]() DE·AD=a,
DE·AD=a,
∴DE=2.
当点F从D到B时,用![]() s,
s,
∴BD=![]() .
.
Rt△DBE中,
BE=![]() .
.
∵ABCD是菱形,
∴EC=a-1,DC=a,
Rt△DEC中,a![]() =2
=2![]() +(a-1)
+(a-1) ![]() ,
,
解得a=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E、F分别是AB、CD上的点,点G是BC的延长线上一点,且∠B=∠DCG=∠D 则下列判断错误的是( )
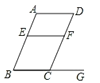
A.∠BEF=∠EFDB.∠A=∠BCFC.∠AEF=∠EBCD.∠BEF+∠EFC=180°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,□ABCD的对角线AC、BD相交于点O,AE=CF.
(1)求证:△BOE≌△DOF;
(2)若BD=EF,连接DE、BF,判断四边形EBFD的形状,并说明理由.

-
科目: 来源: 题型:
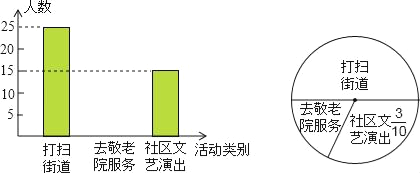
查看答案和解析>>【题目】某中学组织全体学生参加“献爱心”公益活动,为了了解九年级学生参加活动情况,从九年级学生着中随机抽取部分学生进行调查,统计了该天他们打扫街道,去敬老院服务和到社区文艺演出的人数,并绘制了如下不完整的条形统计图和扇形统计图,其中到社区文艺演出的人数占所调查的九年级学生人数的
 ,请根据两幅统计图中的信息,回答下列问题:
,请根据两幅统计图中的信息,回答下列问题:(1)本次调查共抽取了多少名九年级学生?
(2)补全条形统计图.
(3)若该中学九年级共有1500名学生,请你估计该中学九年级去敬老院的学生有多少名?
-
科目: 来源: 题型:
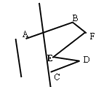
查看答案和解析>>【题目】如图是我校徽标抽象的几何图形,若AB∥CD,∠FED=65°,则∠B+∠F+∠FED+∠D=_________°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形ABC中,∠ABC=105°,过点B作BD⊥AC,垂足为D,E是线段BC上一点,且∠BED=75°,F是射线BA上一点,过点F作FG⊥AC,垂足为G.若∠BDE=55°,则∠BFG=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个商场出售相同的某种商品,每件售价均为3000元,并且多买都有一定的优惠.甲商场的优惠条件是:第一件按原售价收费,其余每件优惠30%;乙商场的优惠条件是:每件优惠25%.设所买商品为x件时,甲商场收费为y1元,乙商场收费为y2元.
(1)分别求出y1,y2与x之间的关系式;
(2)当甲、乙两个商场的收费相同时,所买商品为多少件?
(3)当所买商品为5件时,应选择哪个商场更优惠?请说明理由.
相关试题

