【题目】如图,□ABCD的对角线AC、BD相交于点O,AE=CF.
(1)求证:△BOE≌△DOF;
(2)若BD=EF,连接DE、BF,判断四边形EBFD的形状,并说明理由.

参考答案:
【答案】(1)证明见解析;(2)四边形EBFD为矩形,理由见解析.
【解析】试题分析:(1)先证出OE=OF,再由SAS即可证明△BOE≌△DOF;
(2)由对角线互相平分证出四边形EBFD是平行四边形,再由对角线相等,即可得出四边形EBFD是矩形.
试题解析:(1)证明:∵四边形ABCD为平行四边形,
∴BO=DO,AO=CO.
∵AE=CF,
∴AO-AE=CO-CF,即EO=FO.
在△BOE与△DOF中
∴△BOE≌△DOF.
(2)四边形EBFD为矩形.
∵EO=FO,BO=DO,
∴四边形EBFD为平行四边形.
∵BD=EF,
∴四边形EBFD为矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的腰和底的长分别是一元二次方程x2﹣4x+3=0的根,则该三角形的周长可以是( )
A.5
B.7
C.5或7
D.10 -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场把一个双肩背书包按进价提高50%标价,然后再按八折出售,这样商场每卖出一个书包就可盈利8元.设每个双肩背书包的进价是x元,根据题意列一元一次方程为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC, ∠ABC、∠ACB的三等分线交于点E、D,若∠BFC=132°,∠BGC=118°,则∠A的度数为( )

A.65°
B.66°
C.70°
D.78° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.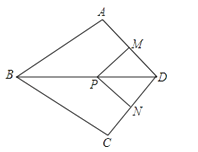
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个两位数,它的个位数与十位数的和是12,而这两个数的积比这个两位数少16 ,这个两位数是____。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.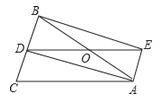
相关试题

