【题目】如图,在⊙O中,直径AB交弦CD于点G,CG=DG,⊙O的切线BE交DO的延长线于点E,F是DE与⊙O的交点,连接BD,BF.
(1)求证:∠CDE=∠E;
(2)若OD=4,EF=1,求CD的长.
参考答案:
【答案】证明:(1)∵在⊙O中,直径AB交弦CD于点G,CG=DG,
∴AB⊥CD,
∵BE是⊙O的切线,
∴AB⊥BE,
∴CD∥BE,
∴∠CDE=∠E;
(2)解:∵∠CDE=∠E,∠DOG=∠BOE,
∴△ODG∽△OEB,
∴![]() ,
,
∵OD=4,EF=1,
∴OB=OF=OD=4,
∴OE=OF+EF=5,
∴![]() ,
,
∴OG=![]() ,
,
∴DG=![]() =
=![]() ,
,
∴CD=2DG=![]() .
.
【解析】(1)由在⊙O中,直径AB交弦CD于点G,CG=DG,根据垂径定理即可得AB⊥CD,又由BE是⊙O的切线,易证得CD∥BE,即可证得结论;
(2)易证得△ODG∽△OEB,然后由相似三角形的对应边成比例,求得OG的长,由勾股定理即可求得DG的长,继而求得答案.
【考点精析】本题主要考查了切线的性质定理的相关知识点,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列变形中:
①由方程
 =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;②由方程
 x=
x= 两边同除以
两边同除以 ,得x=1;
,得x=1;③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣
 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果关于x的分式方程
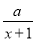 -3=
-3=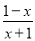 有负分数解,且关于x的不等式组
有负分数解,且关于x的不等式组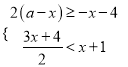 的解集为x<-2,那么符合条件的所有整数a的积是_________.
的解集为x<-2,那么符合条件的所有整数a的积是_________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB

-
科目: 来源: 题型:
查看答案和解析>>【题目】Rt△ABC中,∠ACB=90°,BC=4,如图1,点P从C出发向点B运动,点R是射线PB上一点,PR=3CP,过点R作QR⊥BC,且QR=aCP,连接PQ,当P点到达B点时停止运动.设CP=x,△ABC与△PQR重合部分的面积为S,S关于x的函数图象如图2所示(其中0<x≤
 ,
,  <x≤m,m<x≤n时,函数的解析式不同).
<x≤m,m<x≤n时,函数的解析式不同).
(1)a的值为;
(2)求出S关于x的函数关系式,并写出x的取值范围.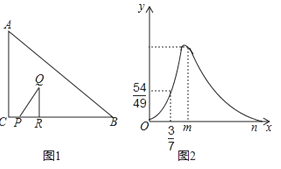
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,点D是AB边上一点(不与AB重合),AD=kBD,过点D作∠EDF+∠C=180°,与CA、CB分别交于E、F.
(1)如图1,当DE=DF时,求 的值.
的值.
(2)如图2,若∠ACB=90°,∠B=30°,DE=m,求DF的长(用含k,m的式子表示)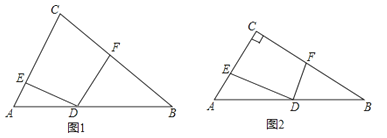
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠BAC=90°,P是BC中点,∠EPF=90°,给出四个结论:①∠B=∠BAP;②AE=CF;③PE=PF;④S四边形AEPF=
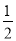 S△ABC.其中成立的有_______
S△ABC.其中成立的有_______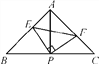
相关试题

