【题目】在△ABC中,点D是AB边上一点(不与AB重合),AD=kBD,过点D作∠EDF+∠C=180°,与CA、CB分别交于E、F.
(1)如图1,当DE=DF时,求![]() 的值.
的值.
(2)如图2,若∠ACB=90°,∠B=30°,DE=m,求DF的长(用含k,m的式子表示)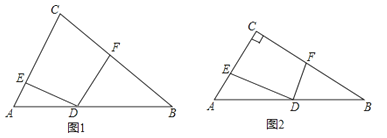
参考答案:
【答案】解:(1)如图1,连接CD,
∵∠EDF+∠C=180°,
∴D,E,C,F四点共圆,
∵DE=DF,
∴∠DCE=∠DCF,
根据正弦定理得![]() ①,
①,![]() ,
,
∴![]() ,②,
,②,
∵∠ADC=180°﹣∠BDC,
∴sin∠ADC=sin∠BDC,
①÷②d得,![]() ,
,
∵AD=kBD,
∴![]() =k;
=k;
(2)∵∠ACB=90°,∠B=30°,
∴∠A=60°,
根据正弦定理得:![]() ③,
③,![]() ,④,
,④,
由(1)知D,E,C,F四点共圆,
∴∠DEA+∠DFB=180°,
∴sin∠DEA=sin∠DFB,④÷③得:![]() ,
,
∴DF=![]() ,
,
∵AD=kBD,DE=m,
∴DF=![]() .
.
【解析】(1)连接CD,由∠EDF+∠C=180°,推出D,E,C,F四点共圆,根据正弦定理得![]() ①,
①,![]() , ②,①÷②得,
, ②,①÷②得,![]() , 根据AD=kBD,根据得到结论;
, 根据AD=kBD,根据得到结论;
(2)根据三角形的内角和得到∠A=60°,根据正弦定理得:![]() ③,
③,![]() , ④,④÷③得:
, ④,④÷③得:![]() , 求得DF=
, 求得DF=![]() , 即可得到结论.
, 即可得到结论.
【考点精析】根据题目的已知条件,利用相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,直径AB交弦CD于点G,CG=DG,⊙O的切线BE交DO的延长线于点E,F是DE与⊙O的交点,连接BD,BF.
(1)求证:∠CDE=∠E;
(2)若OD=4,EF=1,求CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】Rt△ABC中,∠ACB=90°,BC=4,如图1,点P从C出发向点B运动,点R是射线PB上一点,PR=3CP,过点R作QR⊥BC,且QR=aCP,连接PQ,当P点到达B点时停止运动.设CP=x,△ABC与△PQR重合部分的面积为S,S关于x的函数图象如图2所示(其中0<x≤
 ,
,  <x≤m,m<x≤n时,函数的解析式不同).
<x≤m,m<x≤n时,函数的解析式不同).
(1)a的值为;
(2)求出S关于x的函数关系式,并写出x的取值范围.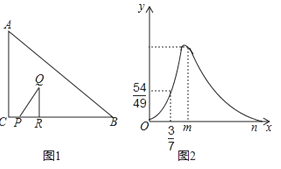
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠BAC=90°,P是BC中点,∠EPF=90°,给出四个结论:①∠B=∠BAP;②AE=CF;③PE=PF;④S四边形AEPF=
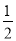 S△ABC.其中成立的有_______
S△ABC.其中成立的有_______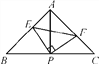
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠E=35°,则∠BAC的度数为( )

A. 40° B. 45° C. 60° D. 70°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△CDE的顶点C点坐标为C(1,﹣2),点D的横坐标为
 , 将△CDE绕点C旋转到△CBO,点D的对应点B在x轴的另一个交点为点A.
, 将△CDE绕点C旋转到△CBO,点D的对应点B在x轴的另一个交点为点A.
(1)图中,∠OCE等于多少;
(2)求抛物线的解析式;
(3)抛物线上是否存在点P,使S△PAE= S△CDE?若存在,直接写出点P的坐标;若不存在,请说明理由.
S△CDE?若存在,直接写出点P的坐标;若不存在,请说明理由.
相关试题

