【题目】如图,在矩形![]() 中,
中,![]() 是
是![]() 上一点,
上一点,![]() 垂直平分
垂直平分![]() ,分别交
,分别交![]() 、
、![]() 、
、![]() 于点
于点![]() 、
、![]() 、
、![]() ,连接
,连接![]() 、
、![]() .
.

(1)求证:![]() ;
;
(2)求证:四边形![]() 是菱形;
是菱形;
(3)若![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() ,求
,求![]() 的长.
的长.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)先根据线段垂直平分线的性质证明PB=PE,由ASA证明△BOQ≌△EOP;
(2)由(1)得出PE=QB,证出四边形BPEQ是平行四边形,再根据菱形的判定即可得出结论;
(3)根据三角形中位线的性质可得AE+BE=2OF+2OB=18,设AE=x,则BE=18x,在Rt△ABE中,根据勾股定理可得![]() ,BE=10,得到
,BE=10,得到![]() ,设PE=y,则AP=8y,BP=PE=y,在Rt△ABP中,根据勾股定理可得
,设PE=y,则AP=8y,BP=PE=y,在Rt△ABP中,根据勾股定理可得![]() ,解得
,解得![]() ,在Rt△BOP中,根据勾股定理可得
,在Rt△BOP中,根据勾股定理可得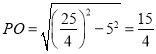 ,由PQ=2PO即可求解.
,由PQ=2PO即可求解.
解:(1)∵![]() 垂直平分
垂直平分![]() ,
,
∴![]() ,
,![]() ,
,
∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∴![]() ,
,
在![]() 与
与![]() 中,
中,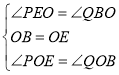 ,
,
∴![]() ,
,
(2)∵![]()
∴![]() ,
,
又∵![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
又∵![]() ,
,
∴四边形![]() 是菱形;
是菱形;
(3)∵![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,
∴![]() ,
,
设![]() ,则
,则![]() ,在
,在![]() 中,
中,![]() ,
,
解得![]() ,
,![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
解得![]() ,
,
在![]() 中,
中,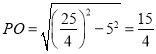 ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将正整数1至2018按一定规律排列如下表:
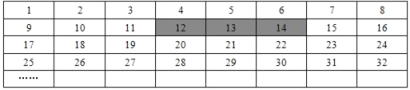
平移表中带阴影的方框,方框中三个数的和可能是( )
A. 2018 B. 2019 C. 2040 D. 2049
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线经过矩形
 的对角线
的对角线 的中点
的中点 ,分别与矩形的两边相交于点
,分别与矩形的两边相交于点 、
、 .
.
(1)求证:
 ;
;(2)若
 ,则四边形
,则四边形 是______形,并说明理由;
是______形,并说明理由;(3)在(2)的条件下,若
 ,
, ,求
,求 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则下列结论:①4ac﹣b2<0;②2a﹣b=0;③a+b+c<0;④点M(x1,y1)、N(x2,y2)在抛物线上,若x1<x2<﹣1,则y1>y2,⑤abc>0.其中正确结论的个数是( )
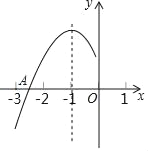
A. 5个 B. 4个 C. 3个 D. 2个
-
科目: 来源: 题型:
查看答案和解析>>【题目】10个人围成一圈做游戏.游戏的规则是:每个人心里都想一个数,并把目己想的数告诉与他相邻的两个人,然后每个人将与他相邻的两个人告诉他的数的平均数报出来,若报出来的数如图所示,则报出来的数是3的人心里想的数是( )

A.2B.
 C.4D.
C.4D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(a,b)为第一象限内一点,且a<b.连结OA,并以点A为旋转中心把OA逆时针转90°后得线段BA.若点A、B恰好都在同一反比例函数的图象上,则
 的值等于___.
的值等于___.
相关试题

