搜索
【题目】若a是方程x2﹣2x﹣1＝0的解，则代数式﹣2a2+4a+2020的值为_____．
参考答案：
【答案】2018．
【解析】
先利用一元二次方程的解的定义得到a2﹣2a＝1，再把﹣2a2+4a+2020变形为﹣2（a2﹣2a）+2020，然后利用整体代入的方法计算．
解：∵a是方程x2﹣2x﹣1＝0的解，
∴a2﹣2a﹣1＝0，
即a2﹣2a＝1，
∴﹣2a2+4a+2020
＝﹣2（a2﹣2a）+2020
＝﹣2×1+2020
＝2018．
故答案为：2018．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某公交公司有A，B型两种客车，它们的载客量和租金如下表：
A
B
载客量（人/辆）
45
30
租金（元/辆）
400
280
学校根据实际情况，计划租用A、B型客车共5辆，同时送八年级师生到素质基地参加社会实践活动，设租用A型客车x辆，根据要求回答下列问题:
（1）用含x的式子填写下表：车辆数（辆）
载客量
租金（元）
A
x
45x
400x
B
5-x
（2）若要保证租车费用不超过1900元，求最多租用A型客车多少辆？
（3）在（2）的条件下，若八年级师生共有195人，写出所有可能的租车方案，并确定最省钱的租车方案。 -
科目： 来源： 题型：
查看答案和解析>>【题目】一粒木质中国象棋棋子“車”，它的正面雕刻一个“車”字，它的反面是平的，将棋子从一定高度下抛，落地反弹后可能是“車”字面朝上，也可能是“車”字面朝下.由于棋子的两面不均匀，为了估计“車”字面朝上的概率，某实验小组做了棋子下抛实验，并把实验数据整理如下：
实验次数
20
40
60
80
100
120
140
160
“車”字面朝上的频数
14
28
38
47
52
66
78
88
相应的频率
0.7
0.7
0.63
0.59
0.52
0.55
0.56
0.55
(1)请将表中数据补充完整，并画出折线统计图中的剩余部分.
(2)如果实验继续进行下去，根据上表数据，这个实验的频率将接近于该事件发生的概率，请估计这个概率是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】(8分)问题情景：某学校数学学习小组在讨论“随机掷二枚均匀的硬币，得到一正一反的概率是多少”时，小聪说：随机掷二枚均匀的硬币，可以有“二正、一正一反、二反”三种情况，所以，P（一正一反）＝
；小颖反驳道：这里的“一正一反”实际上含有“一正一反，一反一正”二种情况，所以P（一正一反）＝
.⑴ 的说法是正确的.
⑵为验证二人的猜想是否正确，小聪与小颖各做了100次实验，得到如下数据：
计算：小聪与小颖二人得到的“一正一反”的频率分别是多少？从他们的实验中，你能得
到“一正一反”的概率是多少吗？
⑶对概率的研究而言小聪与小颖两位同学的实验说明了什么？
-
科目： 来源： 题型：
查看答案和解析>>【题目】从标号分别为1，2，3，4，5的5张卡片中，随机抽取1张．下列事件中，必然事件是【 】
A．标号小于6 B．标号大于6 C．标号是奇数 D．标号是3
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，如图：在平面直角坐标系中，O为坐标原点，四边形OABC是长方形，点A、C、D的坐标分别为A（9，0）、C（0，4），D（5，0），点P从点O出发，以每秒1个单位长度的速度沿O
C B A运动，点P的运动时间为t秒.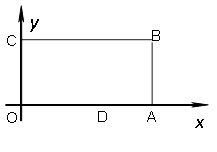
（1）当t=5时， P点坐标为（ ， ）
（2）当t>4时，OP+PD有最小值吗？如果有，请算出该最小值，如果没有，请说明理由。
（3）当t为何值时，△ODP是腰长为5的等腰三角形？（直接写出t的值）。 -
科目： 来源： 题型：
查看答案和解析>>【题目】若α、β是方程x2+2x﹣2017=0的两个实数根，则α2+3α+β的值为 ．
相关试题
