搜索
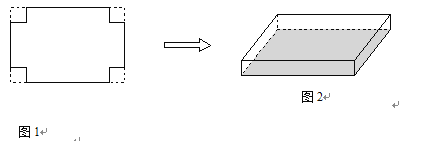
【题目】（本题满分8分）一张长为30cm，宽20cm的矩形纸片，如图1所示，将这张纸片的四个角各剪去一个边长相同的正方形后，把剩余部分折成一个无盖的长方体纸盒，如图1所示，如果折成的长方体纸盒的底面积为264cm2，求剪掉的正方形纸片的边长．
参考答案：
【答案】4cm
【解析】试题分析：设剪掉的正方形纸片的边长为x cm，则围成的长方体纸盒的底面长是（30-2x）cm, 宽是（30-2x）cm,根据底面积等于264 cm2列方程求解.
解：设剪掉的正方形纸片的边长为x cm．
由题意，得 (30-2x)(20-2x)=264．
整理，得 x2 -25x + 84=0．
解方程，得
， 
（不符合题意，舍去）．
答：剪掉的正方形的边长为4cm．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，已知点A（-3，0），B（0，-1），C（0，
）三点．（1）求直线AB的解析式．
（2）若点D在直线AB上，且DB=DC，尺规作图作出点D（保留作图痕迹），并求出点D的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算
（1）（﹣4）2007·（0.25）2018
（2）3（2﹣y）2﹣4（y+5）
（3）（a+2b）（a﹣2b）﹣
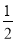b（a﹣8b）（4）（a﹣b）（a2+ab+b2）
-
科目： 来源： 题型：
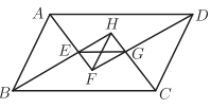
查看答案和解析>>【题目】如图，平行四边形ABCD的四个内角的平分线相交成四边形EFGH，求证：
（1）EG=HF．
（2）EG=BC-AB．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，四边形OBCD是边长为4的正方形，B、D分别在
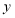轴负半轴、
轴正半轴上，点E是轴的一个动点，连接CE，以CE为边，在直线CE的右侧作正方形CEFG．（1）如图1，当点E与点O重合时，请直接写出点F的坐标为_______，点G的坐标为_______．
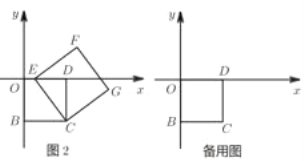
（2）如图2，若点E在线段OD上，且OE=1，求正方形CEFG的面积．
（3）当点E在
轴上移动时，点F是否在某条直线上运动？如果是，请求出相应直线的表达式；如果不是，请说明理由．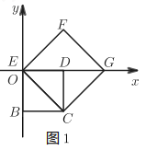
-
科目： 来源： 题型：
查看答案和解析>>【题目】现有190张铁皮做盒子，每张铁皮可做8个盒身或22个盒底，一个盒身与两个盒底配成一个完整的盒子，（一张铁皮只能生产一种产品）
（1）向用多少张铁皮做盒身，多少张铁皮做盒底，可以正好用完190张铁皮并制成一批完整的盒子？
（2）这批盒子一共有多少个？
-
科目： 来源： 题型：
查看答案和解析>>【题目】小林在某商店购买商品A，B共三次，只有其中一次购买时，商品A，B同时打折，其余两次均按标价购买，三次购买商品A、B的数量和费用如表所示，
购买商品A的数量/个
购买商品B的数量/个
购买总费用/元
第一次购物
6
5
1140
第二次购物
3
7
1110
第三次购物
9
8
1062
（1）在这三次购物中，第 次购物打了折扣；
（2）求出商品A、B的标价；
（3）若商品A、B的折扣相同，问商店是打几折出售这两种商品的？
相关试题
