【题目】某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系: 
(1)求出y与x之间的函数关系式;
(2)写出每天的利润W与销售单价x之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少?
参考答案:
【答案】
(1)解:设y与x之间的函数关系式为y=kx+b(k≠0),由所给函数图象可知,
![]() ,
,
解得 ![]() .
.
故y与x的函数关系式为y=﹣x+180
(2)解:∵y=﹣x+180,
∴W=(x﹣100)y=(x﹣100)(﹣x+180)
=﹣x2+280x﹣18000
=﹣(x﹣140)2+1600,
∵a=﹣1<0,
∴当x=140时,W最大=1600,
∴售价定为140元/件时,每天最大利润W=1600元.
【解析】(1)设y与x之间的函数关系式为y=kx+b(k≠0),根据所给函数图象列出关于kb的关系式,求出k、b的值即可;(2)把每天的利润W与销售单价x之间的函数关系式化为二次函数顶点式的形式,由此关系式即可得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用四个长为m,宽为n的相同长方形按如图方式拼成一个正方形.

(1).请用两种不同的方法表示图中阴影部分的面积.
方法①: ;
方法②: .
(2).由 (1)可得出
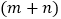 2,
2, ,4mn这三个代数式之间的一个等量关系为: .
,4mn这三个代数式之间的一个等量关系为: .(3)利用(2)中得到的公式解决问题:已知2a+b=6,ab=4,试求
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点E在△ABC内,∠ABC=∠EBD=α,∠ACB=∠EDB=60°,∠AEB=150°,∠BEC=90°.
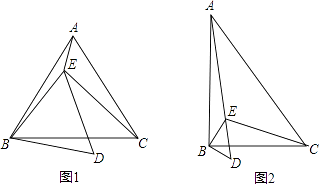
(1)当α=60°时(如图1), ①判断△ABC的形状,并说明理由;
②求证:BD=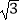 AE;
AE;
(2)当α=90°时(如图2),求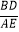 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(概念学习)
规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,如2÷2÷2等.类比有理数的乘方,我们把2÷2÷2记作2③,读作“2的圈3次方”,一般地,把
 (a≠0)记作a,读作“a的圈n次方”.
(a≠0)记作a,读作“a的圈n次方”.(初步探究)
(1)直接写出计算结果:2③=_____,(﹣
 )⑤=_____.
)⑤=_____.(2)关于除方,下列说法准确的选项有_________(只需填入正确的序号)
①.任何非零数的圈2次方都等于1; ②.对于任何正整数n,1=1;
③.3④=4③ ④.负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数.
(深入思考)我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?
例如: 2④=2÷2÷2÷2
=2×
 ×
× ×
×
=(__)2 (幂的形式)
试一试:将下列除方运算直接写成幂的形式.
5⑥=_____;(﹣
 )⑩=_____;a=_____(a≠0).
)⑩=_____;a=_____(a≠0).算一算:
 ④÷23+(﹣8)×2③.
④÷23+(﹣8)×2③. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PB、AB,∠PBA=∠C.

(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为2 ,求BC的长.
,求BC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】化简求值:
(1)
 ,其中
,其中 ;
;(2)若
 ,且
,且 ,求
,求 的值。
的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲、乙分别是4等分、3等分的两个圆转盘,指针固定,转盘转动停止后,指针指向某一数字.
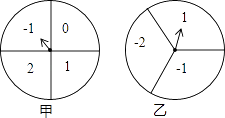
(1)直接写出转动甲盘停止后指针指向数字“1”的概率;
(2)小华和小明利用这两个转盘做游戏,两人分别同时转动甲、乙两个转盘,停止后,指针各指向一个数字,若两数字之积为非负数则小华胜;否则,小明胜.你认为这个游戏公平吗?请你利用列举法说明理由.
相关试题

