【题目】在Rt△ABC中,∠ACB=90°,BC=a,AC=b,AB=c.将Rt△ABC绕点O依次旋转90°、180°和270°,构成的图形如图所示.该图是我国古代数学家赵爽制作的“勾股圆方图”,也被称作“赵爽弦图”,它是我国最早对勾股定理证明的记载,也成为了2002年在北京召开的国际数学家大会的会标设计的主要依据.

(1)请利用这个图形证明勾股定理;
(2)请利用这个图形说明a2+b2≥2ab,并说明等号成立的条件;
(3)请根据(2)的结论解决下面的问题:长为x,宽为y的长方形,其周长为8,求当x,y取何值时,该长方形的面积最大?最大面积是多少?
参考答案:
【答案】(1)详见解析;(2)当且仅当a=b时,等号成立;(3)当且仅当x=y=2时,长方形的面积最大,最大面积是4.
【解析】
1)根据题意,我们可在图中找等量关系,由中间的小正方形的面积等于大正方形的面积减去四个直角三角形的面积,列出等式化简即可得出勾股定理的表达式.
(2)利用非负数的性质证明即可.
(3)利用(2)中的结论求得当x,y取何值时,该矩形面积最大以及其最大面积.
解:(1)因为边长为c的正方形面积为c2,
它也可以看成是由4个直角三角形与1个边长为(a– b)的小正方形组成的,
它的面积为4×![]() ab+(a– b)2=a2+b2,
ab+(a– b)2=a2+b2,
所以c2=a2+b2.
(2)∵(a– b)2≥0,
∴a2+b2–2ab≥0,∴a2+b2≥2ab,
当且仅当a=b时,等号成立.
(3)依题意得2(x+y)=8,∴x+y=4,长方形的面积为xy,
由(2)的结论知2xy≤x2+y2=(x+y)2–2xy,
∴4xy≤(x+y)2,∴xy≤4,
当且仅当x=y=2时,长方形的面积最大,最大面积是4.
-
科目: 来源: 题型:
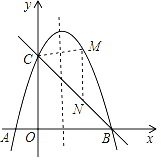
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C,已知A(﹣1,0),C(0,3)
(1)求该抛物线的表达式;
(2)求BC的解析式;
(3)点M是对称轴右侧点B左侧的抛物线上一个动点,当点M运动到什么位置时,△BCM的面积最大?求△BCM面积的最大值及此时点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥BC,DC⊥BC,E是BC上一点,EM⊥EN,∠EMA和∠END的平分线交于点F,则∠F的度数为( )

A. 120° B. 135° C. 150° D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程rx2+(r+2)x+r﹣1=0有根只有整数根的一切有理数r的值有( )个.
A. 1 B. 2 C. 3 D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3,已知A(1,5) 、A1(2,5) 、A2(4,5) 、A3(8,5) 、B(2,0) 、B1(4,0) 、B2(8,0) 、B3(16,0):若按此规律,将△OAB进行n次变换,得到△OAnBn。推测An的坐标是___________,Bn的坐标是___________。( )

A. (2n,5)(2n+1,0) B. (2n-1,5)(2n+1,0) C. (2n,5)(2n,0) D. (2n+1,5)(2n+1,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长均为1,建立如图所示的直角坐标系,已知两点A(0,2),B(4,1)

(1)请在x轴上画出一点P,使得PA+PB的值最小;
(2)请直接写出:点P的坐标 ;PA+PB的最小值为 .
-
科目: 来源: 题型:
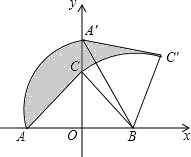
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,在以AB的中点O为坐标原点,AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴的正半轴上的A处,若AO=OB=2,则阴影部分面积为( )
A.
 B.
B.  C.
C.  D.
D. 
相关试题

