【题目】小明在矩形纸片上画正三角形,他的做法是:①对折矩形纸片ABCD(AB>BC),使AB与DC重合,得到折痕EF,把纸片展平;②沿折痕BG折叠纸片,使点C落在EF上的点P处,再折出PB、PC,最后用笔画出△PBC(图1).

(1)求证:图1中的 ![]() PBC是正三角形:
PBC是正三角形:
(2)如图2,小明在矩形纸片HIJK上又画了一个正三角形IMN,其中IJ=6cm,
且HM=JN.
①求证:IH=IJ
②请求出NJ的长;
(3)小明发现:在矩形纸片中,若一边长为6cm,当另一边的长度a变化时,在矩形纸片上总能画出最大的正三角形,但位置会有所不同.请根据小明的发现,画出不同情形的示意图(作图工具不限,能说明问题即可),并直接写出对应的a的取值范围.
参考答案:
【答案】(1)证明见解析;(2)①证明见解析;②12-6![]() (3)3
(3)3![]() <a<4
<a<4![]() ,a>4
,a>4![]()
【解析】(1)由折叠的性质和垂直平分线的性质得出PB=PC,PB=CB,得出PB=PC=CB即可;
(2)①利用“HL”证Rt△IHM≌Rt△IJN即可得;②IJ上取一点Q,使QI=QN,由Rt△IHM≌Rt△IJN知∠HIM=∠JIN=15°,继而可得∠NQJ=30°,设NJ=x,则IQ=QN=2x、QJ=![]() x,根据IJ=IQ+QJ求出x即可得;
x,根据IJ=IQ+QJ求出x即可得;
(3)由等边三角形的性质、直角三角形的性质、勾股定理进行计算,画出图形即可.
(1)证明:∵①对折矩形纸片ABCD(AB>BC),使AB与DC重合,得到折痕EF
∴PB=PC
∵沿折痕BG折叠纸片,使点C落在EF上的点P处
∴PB=BC
∴PB=PC=BC
∴△PBC是正三角形:
(2)证明:①如图
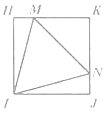
∵矩形AHIJ
∴∠H=∠J=90°
∵△MNJ是等边三角形
∴MI=NI
在Rt△MHI和Rt△JNI中
![]()
∴Rt△MHI≌Rt△JNI(HL)
∴HI=IJ
②在线段IJ上取点Q,使IQ=NQ
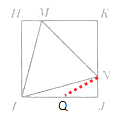
∵Rt△IHM≌Rt△IJN,
∴∠HIM=∠JIN,
∵∠HIJ=90°、∠MIN=60°,
∴∠HIM=∠JIN=15°,
由QI=QN知∠JIN=∠QNI=15°,
∴∠NQJ=30°,
设NJ=x,则IQ=QN=2x,QJ=![]() x,
x,
∵IJ=6cm,
∴2x+![]() x=6,
x=6,
∴x=12-6![]() ,即NJ=12-6
,即NJ=12-6![]() (cm).
(cm).
(3)分三种情况:
①如图:
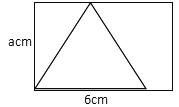
设等边三角形的边长为b,则0<b≤6,
则tan60°=![]() ,
,
∴a=![]() ,
,
∴0<b≤![]() =
=![]() ;
;
②如图
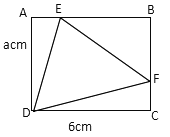
当DF与DC重合时,DF=DE=6,
∴a=sin60°×DE=![]() =
=![]() ,
,
当DE与DA重合时,a=![]() ,
,
∴![]() <a<
<a<![]() ;
;
③如图
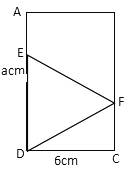
∵△DEF是等边三角形
∴∠FDC=30°
∴DF=![]()
∴a>![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)整式
 表示
表示 、
、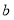 两数和的平方
两数和的平方整式
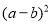 表示
表示 、
、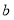 两数差的平方
两数差的平方仿照上例填空:整式
 表示:______.
表示:______.整式
 表示:______.
表示:______.(2)试计算
 、
、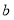 取不同数值时,
取不同数值时, 及
及 的值填入下表:
的值填入下表: 、
、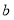 的值
的值当
 ,
, 时
时当
 ,
,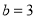 时
时当
 ,
, 时
时当
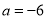 ,
, 时
时

(3)根据上表,我发现的规律______.
(4)用发现的规律计算:

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司对一款新高压锅进行测试,放入足量的水和设定某一模式后,在容积不变的情况下,根据温度t(℃)的变化测出高压锅内的压强p(kpa)的大小.压强在加热前是100kpa,达到最大值后高压锅停止加热。为方便分析,测试员记y=p-100,
表示压强在测试过程中相对于100kpa的增加值.部分数据如下表:

温度f(℃)
0
10
20
30
40
50
60
压强增加值
Y(kpa)
0
9.5
18
25.5
32
37.5
42
(1)根据表中的数据,在给出的坐标系中画出相应的点(坐标系已画在答卷上);
(2)y与t之问是否存在函数关系?若是,请求出函数关系式;否则请说明理由;
(3)①在该模式下,压强P的最大值是多少?
②当t分别为,t1,t2(t1<t2)时,对应y的值分别为y1 ,y2 , 请比较
 与
与 的大小,并解释比较结果的实际意义.
的大小,并解释比较结果的实际意义. -
科目: 来源: 题型:
查看答案和解析>>【题目】下表是今年雨季某河流一周的水位变化情况(上周末的水位达到警戒水位)
星期
一
二
三
四
五
六
日
水位记录
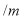
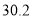

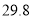
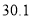
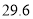
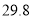
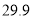
注:此河流的警戒水位为
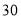 米.
米.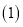 完成下面的本周水位变化记录表:
完成下面的本周水位变化记录表:星期
一
二
三
四
五
六
日
水位变化
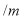 (与前一天比较)
(与前一天比较)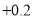
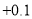
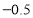
(注:规定水位比前一天上升用“
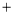 ”,水位比前一天下降用“
”,水位比前一天下降用“ ”,不升不降记作“
”,不升不降记作“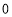 ”.)
”.) 与上周末相比,本周末河流水位是上升了还是下降了? (填“上升”或“下降”)
与上周末相比,本周末河流水位是上升了还是下降了? (填“上升”或“下降”) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平整的地面上,用
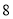 个棱长都为
个棱长都为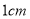 的小正方体堆成一个几何体.
的小正方体堆成一个几何体.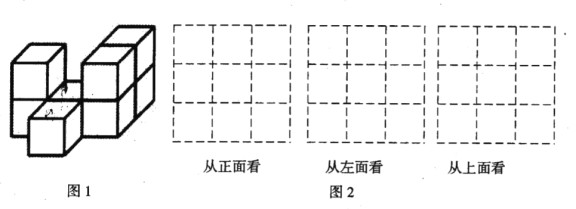
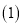 请在图2中画出从正面、左面和上面看到的这个几何体的形状图;
请在图2中画出从正面、左面和上面看到的这个几何体的形状图; 如果现在你还有一些大小相同的小正方体,要求保持从上面和左面看到的形状图都不变,最多可以再添加 个小正方体;
如果现在你还有一些大小相同的小正方体,要求保持从上面和左面看到的形状图都不变,最多可以再添加 个小正方体;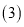 图1中
图1中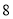 个小正方体搭成的几何体的表面积(包括与地面接触的部分)是
个小正方体搭成的几何体的表面积(包括与地面接触的部分)是 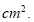
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,点P的坐标为(m,n),则向量
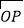 可以用点P的坐标表示为
可以用点P的坐标表示为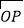 =(m,n);已知
=(m,n);已知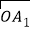 =(x1,y1),
=(x1,y1),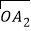 =(x2,y2),若x1x2+y1y2=0,则
=(x2,y2),若x1x2+y1y2=0,则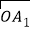 与
与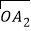 互相垂直.
互相垂直.下面四组向量:①
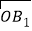 =(3,﹣9),
=(3,﹣9),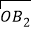 =(1,﹣
=(1,﹣ );
);②
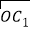 =(2,π0),
=(2,π0),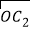 =(2﹣1,﹣1);
=(2﹣1,﹣1);③
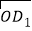 =(cos30°,tan45°),
=(cos30°,tan45°),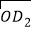 =(sin30°,tan45°);
=(sin30°,tan45°);④
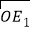 =(
=(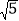 +2,
+2,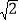 ),
),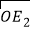 =(
=(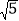 ﹣2,
﹣2, ).
).其中互相垂直的组有( )
A. 1组 B. 2组 C. 3组 D. 4组
-
科目: 来源: 题型:
查看答案和解析>>【题目】八(6)班为从甲、乙两同学中选出班长,进行了一次演讲答辩和民主测评.其中,A、B、C、D、E五位老师作为评委,对演讲答辩情况进行评价,结果如下表;另全班50位同学参与民主测评进行投票,结果如下图:

A
B
C
D
E
甲
89
91
92
94
93
乙
90
86
85
91
94

规定: 演讲得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;民主测评得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分.
(1)求甲、乙两位选手各自演讲答辩的平均分;
(2)民主测评统计图中a= ,b= ;
(3)求甲、乙两位选手的民主测评得分;
(4)若按演讲答辩得分和民主测评6:4的权重比计算两位选手的综合得分,则应选取哪位选手当班长?
相关试题

