【题目】(1)整式![]() 表示
表示![]() 、
、![]() 两数和的平方
两数和的平方
整式![]() 表示
表示![]() 、
、![]() 两数差的平方
两数差的平方
仿照上例填空:整式![]() 表示:______.
表示:______.
整式![]() 表示:______.
表示:______.
(2)试计算![]() 、
、![]() 取不同数值时,
取不同数值时,![]() 及
及![]() 的值填入下表:
的值填入下表:
| 当 | 当 | 当 | 当 |
| ||||
|
(3)根据上表,我发现的规律______.
(4)用发现的规律计算:![]()
参考答案:
【答案】(1)整式![]() 表示
表示![]() 、
、![]() 两数平方的差.整式
两数平方的差.整式![]() 表示
表示![]() 、
、![]() 两数和与
两数和与![]() 、
、![]() 两数差的积;(2)5,16,7,36;5,16,7,36;(3)
两数差的积;(2)5,16,7,36;5,16,7,36;(3)![]() ;(4)3654
;(4)3654
【解析】
(1)根据两式的意义即可写出结论;
(2)分别代入求值即可;
(3)根据前边的计算,总结出a2﹣b2与(a+b)(a﹣b)的大小关系即可;
(4)利用(3)中的关系,计算即可.
(1)整式![]() 表示
表示![]() 、
、![]() 两数平方的差.整式
两数平方的差.整式![]() 表示
表示![]() 、
、![]() 两数和与
两数和与![]() 、
、![]() 两数差的积.
两数差的积.
(2)
| 当 | 当 | 当 | 当 |
| 5 | 16 | 7 | 36 |
| 5 | 16 | 7 | 36 |
(3)根据上表,我发现的规律是![]()
(4)![]()
![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市共有一中、二中、三中等3所高中,有一天所有高二学生参加了一次数学测试,阅卷后老师们对第10题进行了分析,把每个学生的解答情况归结为下列四类情况之一:A(概念错误),B(计算错误),C(基本正确),D(完全正确).各校出现这四类情况的人数占本校高二学生数的百分比见下面的条形统计图:
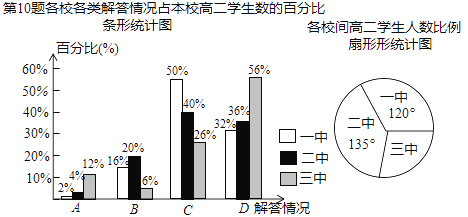
已知一中高二学生有400名,这三所学校之问高二学生人数的比例见扇形统计图.
(1)求全市高二学生总数;
(2)求全市解答完全正确的高二学生数占高二学生总数的百分比;
(3)请你对三中高二数学老师提一个值得关注的教学建议,并说明理由.
-
科目: 来源: 题型:
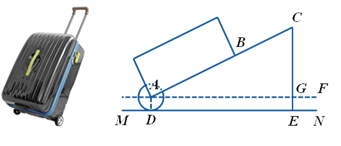
查看答案和解析>>【题目】有一只拉杆式旅行箱(图1),其侧面示意图如图2所示.已知箱体长AB=50cm,拉杆
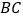 的伸长距离最大时可达35cm,点A,B,C在同一条直线上.在箱体底端装有圆形的滚轮⊙A,⊙A与水平地面MN相切于点D.在拉杆伸长至最大的情况下,当点B距离水平地面38cm时,点C到水平地面的距离CE为59cm.
的伸长距离最大时可达35cm,点A,B,C在同一条直线上.在箱体底端装有圆形的滚轮⊙A,⊙A与水平地面MN相切于点D.在拉杆伸长至最大的情况下,当点B距离水平地面38cm时,点C到水平地面的距离CE为59cm.设AF∥MN.
(1)求⊙A的半径长;
(2)当人的手自然下垂拉旅行箱时,人感到较为舒服.某人将手自然下垂在C端拉旅行箱时,CE为80cm,
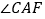 =64°.求此时拉杆BC的伸长距离.(精确到1cm,参考数据:
=64°.求此时拉杆BC的伸长距离.(精确到1cm,参考数据: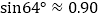 ,
,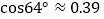 ,
,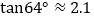 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,AD∥BC,AD=5,B(-3,0),C(9,0),点E是BC的中点,点P是线段BC上一动点,当PB=________时,以点P、A、D、E为顶点的四边形是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司对一款新高压锅进行测试,放入足量的水和设定某一模式后,在容积不变的情况下,根据温度t(℃)的变化测出高压锅内的压强p(kpa)的大小.压强在加热前是100kpa,达到最大值后高压锅停止加热。为方便分析,测试员记y=p-100,
表示压强在测试过程中相对于100kpa的增加值.部分数据如下表:

温度f(℃)
0
10
20
30
40
50
60
压强增加值
Y(kpa)
0
9.5
18
25.5
32
37.5
42
(1)根据表中的数据,在给出的坐标系中画出相应的点(坐标系已画在答卷上);
(2)y与t之问是否存在函数关系?若是,请求出函数关系式;否则请说明理由;
(3)①在该模式下,压强P的最大值是多少?
②当t分别为,t1,t2(t1<t2)时,对应y的值分别为y1 ,y2 , 请比较
 与
与 的大小,并解释比较结果的实际意义.
的大小,并解释比较结果的实际意义. -
科目: 来源: 题型:
查看答案和解析>>【题目】下表是今年雨季某河流一周的水位变化情况(上周末的水位达到警戒水位)
星期
一
二
三
四
五
六
日
水位记录
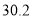

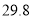
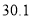
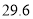
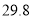
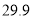
注:此河流的警戒水位为
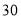 米.
米.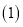 完成下面的本周水位变化记录表:
完成下面的本周水位变化记录表:星期
一
二
三
四
五
六
日
水位变化
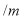 (与前一天比较)
(与前一天比较)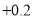
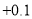
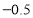
(注:规定水位比前一天上升用“
 ”,水位比前一天下降用“
”,水位比前一天下降用“ ”,不升不降记作“
”,不升不降记作“ ”.)
”.) 与上周末相比,本周末河流水位是上升了还是下降了? (填“上升”或“下降”)
与上周末相比,本周末河流水位是上升了还是下降了? (填“上升”或“下降”) -
科目: 来源: 题型:
查看答案和解析>>【题目】小明在矩形纸片上画正三角形,他的做法是:①对折矩形纸片ABCD(AB>BC),使AB与DC重合,得到折痕EF,把纸片展平;②沿折痕BG折叠纸片,使点C落在EF上的点P处,再折出PB、PC,最后用笔画出△PBC(图1).

(1)求证:图1中的
 PBC是正三角形:
PBC是正三角形: (2)如图2,小明在矩形纸片HIJK上又画了一个正三角形IMN,其中IJ=6cm,
且HM=JN.
①求证:IH=IJ
②请求出NJ的长;
(3)小明发现:在矩形纸片中,若一边长为6cm,当另一边的长度a变化时,在矩形纸片上总能画出最大的正三角形,但位置会有所不同.请根据小明的发现,画出不同情形的示意图(作图工具不限,能说明问题即可),并直接写出对应的a的取值范围.
相关试题

