【题目】已知实数a , b满足a-b=1,a2-ab+2>0,当1≤x≤2时,函数y= ![]() (a≠0)的最大值与最小值之差是1,求a的值
(a≠0)的最大值与最小值之差是1,求a的值
参考答案:
【答案】解答:∵a2-ab+2>0,
∴a2-ab>-2,
a(a-b)>-2,
∵a-b=1,
∴a>-2,
① -2<a<0,1≤x≤2时,函数y= ![]() 的最大值是y=
的最大值是y= ![]() ,最小值是y=a ,
,最小值是y=a ,
∵最大值与最小值之差是1,
∴ ![]() -a=1,
-a=1,
解得:a=-2,不合题意,舍去;
②当a>0,1≤x≤2时,函数y= ![]() 的最大值是y=a , 最小值是y=
的最大值是y=a , 最小值是y= ![]() ∵最大值与最小值之差是1,
∵最大值与最小值之差是1,
∴a- ![]() =1,
=1,
解得:a=2,符合题意,
∴a的值是2.
【解析】首先根据条件a-b=1,a2-ab+2>0可确定a>-2,然后再分情况进行讨论:①当-2<a<0,1≤x≤2时,函数y= ![]() 的最大值是y=
的最大值是y= ![]() ,最小值是y=a , ②当a>0,1≤x≤2时,函数y=
,最小值是y=a , ②当a>0,1≤x≤2时,函数y= ![]() 的最大值是y=a , 最小值是y=
的最大值是y=a , 最小值是y= ![]() ,再分别根据最大值与最小值之差是1,计算出a的值
,再分别根据最大值与最小值之差是1,计算出a的值
【考点精析】根据题目的已知条件,利用反比例函数的图象和反比例函数的性质的相关知识可以得到问题的答案,需要掌握反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点;性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学在计算一个多项式乘以﹣3x2时,因抄错运算符号,算成了加上﹣3x2,得到的结果是x2﹣4x+1,那么正确的计算结果是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角三角形中,两个锐角的度数比为2:3,则较小锐角的度数为( )
A.20°
B.32°
C.36°
D.72° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC是直角三角形,且∠C=Rt∠,若∠A=34°,则∠B=( )
A.66°
B.56°
C.46°
D.146° -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组线段中的三个长度:①9,12,15;②7,24,25;③32,42,52;④3a,4a,5a(a>0);⑤m2﹣n2,2mn,m2+n2(m,n为正整数,且m>n)其中可以构成直角三角形的有( )
A. 5组 B. 4组 C. 3组 D. 2组
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下列推理说明:
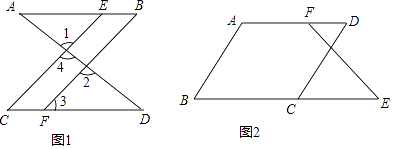
(1)如图1,已知∠1=∠2,∠B=∠C,可推出AB∥CD.理由如下: 因为∠1=∠2(已知),且∠1=∠4()
所以∠2=∠4(等量代换)
所以CE∥BF()
所以∠=∠3()
又因为∠B=∠C(已知)
所以∠3=∠B(等量代换)
所以AB∥CD()
(2)如图2,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE. 证明:∵∠B+∠BCD=180°(已知),
∴AB∥CD ()
∴∠B=()
又∵∠B=∠D(已知),
∴∠=∠(等量代换)
∴AD∥BE()
∴∠E=∠DFE() -
科目: 来源: 题型:
查看答案和解析>>【题目】绝对值等于其相反数的数一定是( )
A.负数
B.正数
C.负数或零
D.正数或零
相关试题

