【题目】下列各组线段中的三个长度:①9,12,15;②7,24,25;③32,42,52;④3a,4a,5a(a>0);⑤m2﹣n2,2mn,m2+n2(m,n为正整数,且m>n)其中可以构成直角三角形的有( )
A. 5组 B. 4组 C. 3组 D. 2组
参考答案:
【答案】B
【解析】①中有92+122=152;
②中有72+242=252;
③(32)2+(42)2≠(52)2;
④中有(3a)2+(4a)2=(5a)2;
⑤中有(m2n2)2+(2mn)2=(m2+n2)2,所以可以构成4组直角三角形.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角三角形中,两个锐角的度数比为2:3,则较小锐角的度数为( )
A.20°
B.32°
C.36°
D.72° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC是直角三角形,且∠C=Rt∠,若∠A=34°,则∠B=( )
A.66°
B.56°
C.46°
D.146° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知实数a , b满足a-b=1,a2-ab+2>0,当1≤x≤2时,函数y=
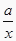 (a≠0)的最大值与最小值之差是1,求a的值
(a≠0)的最大值与最小值之差是1,求a的值 -
科目: 来源: 题型:
查看答案和解析>>【题目】完成下列推理说明:
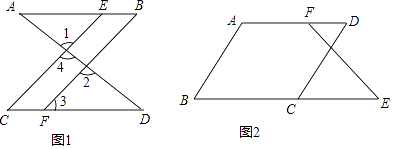
(1)如图1,已知∠1=∠2,∠B=∠C,可推出AB∥CD.理由如下: 因为∠1=∠2(已知),且∠1=∠4()
所以∠2=∠4(等量代换)
所以CE∥BF()
所以∠=∠3()
又因为∠B=∠C(已知)
所以∠3=∠B(等量代换)
所以AB∥CD()
(2)如图2,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE. 证明:∵∠B+∠BCD=180°(已知),
∴AB∥CD ()
∴∠B=()
又∵∠B=∠D(已知),
∴∠=∠(等量代换)
∴AD∥BE()
∴∠E=∠DFE() -
科目: 来源: 题型:
查看答案和解析>>【题目】绝对值等于其相反数的数一定是( )
A.负数
B.正数
C.负数或零
D.正数或零 -
科目: 来源: 题型:
查看答案和解析>>【题目】若直角三角形中的两个锐角之差为16°,则较大的一个锐角的度数是( )
A.37°
B.53°
C.26°
D.63°
相关试题

