搜索
【题目】八年级某班40名学生的数学测试成绩分为5组，第1﹣4组的频数分别为12，10，6，8，则第5组的频率是（ ）
A. 0.1 B. 0.2 C. 0.3 D. 0.4
参考答案：
【答案】A
【解析】
直接利用频数÷总数=频率，进而得出答案．
解：∵八年级某班40名学生的数学测试成绩分为5组，第1﹣4组的频数分别为12，10，6，8，
∴第5组的频率是：（40﹣12﹣10﹣6﹣8）÷40=0.1．
故选：A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，边长为a的等边△ACB中，E是对称轴AD上一个动点，连EC，将线段EC绕点C逆时针旋转60°得到MC，连DM，则在点E运动过程中，DM的最小值是_____。
【答案】1.5
【解析】试题分析：取AC的中点G，连接EG，根据等边三角形的性质可得CD=CG，再求出∠DCF=∠GCE，根据旋转的性质可得CE=CF，然后利用“边角边”证明△DCF和△GCE全等，再根据全等三角形对应边相等可得DF=EG，然后根据垂线段最短可得EG⊥AD时最短，再根据∠CAD=30°求解即可．
解：如图，取AC的中点G，连接EG，
∵旋转角为60°，
∴∠ECD+∠DCF=60°，
又∵∠ECD+∠GCE=∠ACB=60°，
∴∠DCF=∠GCE，
∵AD是等边△ABC的对称轴，
∴CD=
BC，∴CD=CG，
又∵CE旋转到CF，
∴CE=CF，
在△DCF和△GCE中，
，∴△DCF≌△GCE（SAS），
∴DF=EG，
根据垂线段最短，EG⊥AD时，EG最短，即DF最短，
此时∵∠CAD=
×60°=30°，AG=AC=×6=3，∴EG=
AG=×3=1.5，∴DF=1.5．
故答案为：1.5．
考点：旋转的性质；等边三角形的性质．
【题型】填空题
【结束】
19【题目】分解因式：
(1)
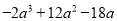； (2)9(m+n)2﹣16(m﹣n)2. -
科目： 来源： 题型：
查看答案和解析>>【题目】解方程：（1）
（2）x2－2x－4＝0（3）x2﹣4x+1=0（用配方法） （4）
-
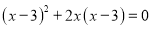
科目： 来源： 题型：
查看答案和解析>>【题目】计算x3x2的结果是（ ）
A.x
B.x5
C.x6
D.x9 -
科目： 来源： 题型：
查看答案和解析>>【题目】分解因式：
(1)
； (2)9(m+n)2﹣16(m﹣n)2.【答案】（1）-2a(a-3)2 ;（2）-(7m-n)(m-7n).
【解析】试题分析：因式分解的常用方法：提取公因式法，公式法，十字相乘法，分组分解法.
试题解析：（1）原式
（2）原式
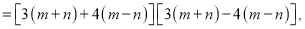
点睛：因式分解的常用方法：提取公因式法，公式法，十字相乘法，分组分解法.
【题型】解答题
【结束】
20【题目】计算:
（1）
； （2）
；（3）
； （4）[（xy+2）（xy－2）－2x2y2+4]÷xy. -
科目： 来源： 题型：
查看答案和解析>>【题目】计算：16+（﹣25）+24﹣15．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一条公路的转弯处是一段圆弧AB．
（1）作出弧AB所在圆的圆心O；（用直尺和圆规作图，保留作图痕迹，不写作法）
（2）若弧AB的中点C到弦AB的距离为20m，AB=80m，求弧AB所在圆的半径．
相关试题
