搜索
【题目】解方程：（1）
（2）x2－2x－4＝0
（3）x2﹣4x+1=0（用配方法） （4）
参考答案：
【答案】（1）x1=2，x2=﹣1；（2）x1=1+
，x2=1﹣
；（3）x1=2+
，x2=2﹣
；（4）x1=3，x2=1
【解析】试题分析：（1）移项后开方，即可得出两个一元一次方程，求出方程的解即可；
（2）求出b2﹣4ac的值，再代入公式求出即可；
（3）移项，配方，开方，即可得出两个一元一次方程，求出方程的解即可；
（4）先分解因式，即可得出两个一元一次方程，求出方程的解即可．
试题解析：（1）（2x﹣1）2﹣9=0，
（2x﹣1）2=9，
2x﹣1=±3，
x1=2，x2=﹣1；
（2）x2﹣2x﹣4=0
b2﹣4ac=（﹣2）2﹣4×1×（﹣4）=20，
x=
，
x1=1+
，x2=1﹣
；
（3）x2﹣4x+1=0，
x2﹣4x=﹣1，
x2﹣4x+4=﹣1+4，
（x﹣2）2=3，
x﹣2=
，
x1=2+
，x2=2﹣
；
（4）（x﹣3）2+2x（x﹣3）=0，
（x﹣3）（x﹣3+2x）=0，
x﹣3=0，x﹣3+2x=0，
x1=3，x2=1．
-
科目： 来源： 题型：
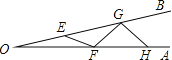
查看答案和解析>>【题目】如图，∠AOB是一角度为10°的钢架，要使钢架更加牢固，需在其内部添加一些钢管：EF、FG、GH…，且OE=EF=FG=GH…，在OA、OB足够长的情况下，最多能添加这样的钢管的根数为 _________．
【答案】8
【解析】添加的钢管长度都与OE相等，∠AOB=10°，根据三角形外角的性质和等腰三角形的性质可得∠GEF=∠FGE=20°，再由三角形外角的性质和等腰三角形的性质可得∠GFH=∠GHF=30°，……，由此规律可得：第一个等腰三角形的底角是10°，第二个是20°，第三个是30°，第四个是40°，第五个是50°，第六个是60°，第七个是70°，第八个是80°，第九个是90°，不符合三角形的内角和定理，不存在．所以一共有8个．
点睛：此题考查了三角形的内角和定理和等腰三角形的性质及三角形外角的性质；发现并利用规律是正确解答本题的关键．
【题型】填空题
【结束】
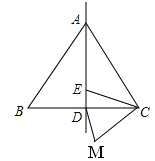
18【题目】如图，边长为a的等边△ACB中，E是对称轴AD上一个动点，连EC，将线段EC绕点C逆时针旋转60°得到MC，连DM，则在点E运动过程中，DM的最小值是_____。
-
科目： 来源： 题型：
查看答案和解析>>【题目】观察下列各式：﹣1+2=1；﹣1+2﹣3+4=2；﹣1+2﹣3+4﹣5+6=3…那么﹣5+6﹣7+8﹣9+10﹣…﹣2015+2016﹣2017+2018= ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，边长为a的等边△ACB中，E是对称轴AD上一个动点，连EC，将线段EC绕点C逆时针旋转60°得到MC，连DM，则在点E运动过程中，DM的最小值是_____。
【答案】1.5
【解析】试题分析：取AC的中点G，连接EG，根据等边三角形的性质可得CD=CG，再求出∠DCF=∠GCE，根据旋转的性质可得CE=CF，然后利用“边角边”证明△DCF和△GCE全等，再根据全等三角形对应边相等可得DF=EG，然后根据垂线段最短可得EG⊥AD时最短，再根据∠CAD=30°求解即可．
解：如图，取AC的中点G，连接EG，
∵旋转角为60°，
∴∠ECD+∠DCF=60°，
又∵∠ECD+∠GCE=∠ACB=60°，
∴∠DCF=∠GCE，
∵AD是等边△ABC的对称轴，
∴CD=
BC，∴CD=CG，
又∵CE旋转到CF，
∴CE=CF，
在△DCF和△GCE中，
，∴△DCF≌△GCE（SAS），
∴DF=EG，
根据垂线段最短，EG⊥AD时，EG最短，即DF最短，
此时∵∠CAD=
×60°=30°，AG=AC=×6=3，∴EG=
AG=×3=1.5，∴DF=1.5．
故答案为：1.5．
考点：旋转的性质；等边三角形的性质．
【题型】填空题
【结束】
19【题目】分解因式：
(1)
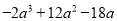； (2)9(m+n)2﹣16(m﹣n)2. -
科目： 来源： 题型：
查看答案和解析>>【题目】计算x3x2的结果是（ ）
A.x
B.x5
C.x6
D.x9 -
科目： 来源： 题型：
查看答案和解析>>【题目】八年级某班40名学生的数学测试成绩分为5组，第1﹣4组的频数分别为12，10，6，8，则第5组的频率是（ ）
A. 0.1 B. 0.2 C. 0.3 D. 0.4
-
科目： 来源： 题型：
查看答案和解析>>【题目】分解因式：
(1)
； (2)9(m+n)2﹣16(m﹣n)2.【答案】（1）-2a(a-3)2 ;（2）-(7m-n)(m-7n).
【解析】试题分析：因式分解的常用方法：提取公因式法，公式法，十字相乘法，分组分解法.
试题解析：（1）原式
（2）原式
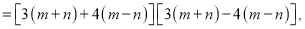
点睛：因式分解的常用方法：提取公因式法，公式法，十字相乘法，分组分解法.
【题型】解答题
【结束】
20【题目】计算:
（1）
； （2）
；（3）
； （4）[（xy+2）（xy－2）－2x2y2+4]÷xy.
相关试题
