【题目】“五一”期间,部分同学随家长一同到某公园游玩,下面是购买门票时,甲同学与其爸爸的对话(如图),试根据图中的信息,解决下列问题:
(1)本次共去了几个成人,几个学生?
(2)甲同学所说的另一种购票方式,是否可以省钱?试说明理由.

参考答案:
【答案】(1)他们一共去了8个成人,4个学生;(2)按团体票购票可以省钱,理由见解析.
【解析】
(1)设去了x个成人,则去了y个学生,根据总人数和总花费建立一个关于x、y的二元一次方程组,然后求解即可得;
(2)另一种购票方式是按团体票购买,先计算出按团体票购票时的总花费,再与800元进行比较即可得出答案.
(1)设去了x个成人,则去了y个学生
依题意得![]()
解得![]()
答:他们一共去了8个成人,4个学生;
(2)若按团体票购票,共需花费的钱数为![]() (元)
(元)
因![]()
故按团体票购票可以省钱.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为节约能源,优化电力资源配置,提高电力供应的整体效益,国家实行了错峰用电.某地区的居民用电,按白天时段和晚间时段规定了不同的单价.某户5月份白天时段用电量比晚间时段用电量多
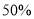 ,6月份白天时段用电量比5月份白天时段用电量少
,6月份白天时段用电量比5月份白天时段用电量少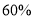 ,结果6月份的总用电量比5月份的总用电量多
,结果6月份的总用电量比5月份的总用电量多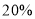 ,但6月份的电费却比5月份的电费少
,但6月份的电费却比5月份的电费少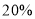 ,则该地区晚间时段居民用电的单价比白天时段的单价低的百分数为( )
,则该地区晚间时段居民用电的单价比白天时段的单价低的百分数为( )A.
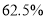 B.
B.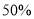 C.
C.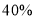 D.
D.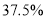
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是某同学对多项式(x2-2x)(x2-2x+2)+1进行因式分解的过程:
解:设x2-2x=y
原式=y (y+2)+1 (第一步)
=y2+2y+1 (第二步)
=(y+1)2 (第三步)
=(x2-2x+1)2 (第四步)
请问:
(1)该同学因式分解的结果是否彻底? (填“彻底”或“不彻底”),若不彻底,则该因式分解的最终结果为 ;
(2)请你模仿上述方法,对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)(发现)如图①,已知等边△ABC,将直角三角板的60°角顶点D任意放在BC边上(点D不与点B、C重合),使两边分别交线段AB、AC于点E、F.
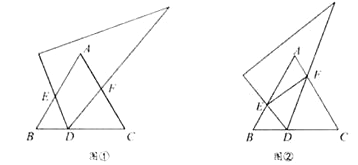
①若AB=6,AE=4,BD=2,则CF =________;
②求证:△EBD∽△DCF.
(2)(思考)若将图①中的三角板的顶点D在BC边上移动,保持三角板与边AB、AC的两个交点E、F都存在,连接EF,如图②所示.问点D是否存在某一位置,使ED平分∠BEF且FD平分∠CFE?若存在,求出
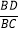 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(3)(探索)如图③,在等腰△ABC中,AB=AC,点O为BC边的中点,将三角形透明纸板的一个顶点放在点O处(其中∠MON=∠B),使两条边分别交边AB、AC于点E、F(点E、F均不与△ABC的顶点重合),连接EF.设∠B=α,则△AEF与△ABC的周长之比为________(用含α的表达式表示)
.
-
科目: 来源: 题型:
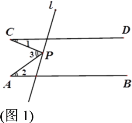
查看答案和解析>>【题目】已知直线AB∥CD,点P为直线l上一点,尝试探究并解答:
(1)如图1,若点P在两平行线之间,∠1=23°,∠2=35°,则∠3= ;
(2)探究图1中∠1,∠2与∠3之间的数量关系,并说明理由;
(3)如图2,若点P在CD的上方,探究∠1,∠2与∠3之间有怎样的数量关系,并说明理由;
(4)如图3,若∠PCD与∠PAB的平分线交于点P1,∠DCP1与∠BAP1的平分线交于点P2,∠DCP2与∠BAP2的平分线交于点P3,…,∠DCPn-1与∠BAPn-1的平分线交于点Pn,若∠PCD=α,∠PAB=β,直接写出∠APnC的度数(用含α与β的代数式表示).


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,D,E分别为AB,AC上一点,将△BCD,△ADE分别沿CD,DE折叠,点A、B恰好重合于点A'处.若∠A'CA=18°,则∠A=____°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在平面直角坐标系xOy 中,抛物线y=ax2+bx+3经过点A(-1,0) 、B(3,0) 两点,且与y轴交于点C
.
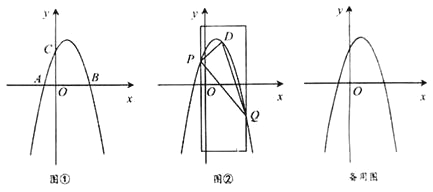
(1)求抛物线的表达式;
(2)如图②,用宽为4个单位长度的直尺垂直于x轴,并沿x轴左右平移,直尺的左右两边所在的直线与抛物线相交于P、 Q两点(点P在点Q的左侧),连接PQ,在线段PQ上方抛物线上有一动点D,连接DP、DQ.
①若点P的横坐标为
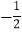 ,求△DPQ面积的最大值,并求此时点D 的坐标;
,求△DPQ面积的最大值,并求此时点D 的坐标;②直尺在平移过程中,△DPQ面积是否有最大值?若有,求出面积的最大值;若没有,请说明理由.
相关试题

