【题目】为节约能源,优化电力资源配置,提高电力供应的整体效益,国家实行了错峰用电.某地区的居民用电,按白天时段和晚间时段规定了不同的单价.某户5月份白天时段用电量比晚间时段用电量多![]() ,6月份白天时段用电量比5月份白天时段用电量少
,6月份白天时段用电量比5月份白天时段用电量少![]() ,结果6月份的总用电量比5月份的总用电量多
,结果6月份的总用电量比5月份的总用电量多![]() ,但6月份的电费却比5月份的电费少
,但6月份的电费却比5月份的电费少![]() ,则该地区晚间时段居民用电的单价比白天时段的单价低的百分数为( )
,则该地区晚间时段居民用电的单价比白天时段的单价低的百分数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
参考答案:
【答案】A
【解析】
设该地区白天时段居民用电的单价为a,晚间用电的单价为b,该户5月份晚间时段用电量为x,先根据题意分别求出5月份白天时段用电量、6月份白天时段和晚间时段用电量,再根据“6月份的电费却比5月份的电费少![]() ”列出方程,求出a、b的关系,从而可得出答案.
”列出方程,求出a、b的关系,从而可得出答案.
设该地区白天时段居民用电的单价为a,晚间用电的单价为b,该户5月份晚间时段用电量为x,则5月份白天时段用电量为![]() ,5月份的总用电量为
,5月份的总用电量为![]()
由题意得:该户6月份白天时段用电量为![]() ,6月份的总用电量为
,6月份的总用电量为![]() ,则6月份晚间时段用电量为
,则6月份晚间时段用电量为![]()
因此,该户5月份的电费为![]() ;6月份的电费为
;6月份的电费为![]()
则有:![]()
解得:![]() ,即
,即![]()
则 ,即晚间用电的单价比白天用电的单价低
,即晚间用电的单价比白天用电的单价低![]()
故选:A.
-
科目: 来源: 题型:
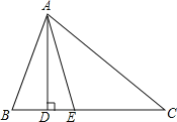
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC,AE平分∠BAC
(1)若∠B=70°,∠C=30°,求;
①∠BAE的度数.
②∠DAE的度数.
(2)探究:如果只知道∠B=∠C+40°,那么能求岀∠DAE的度数吗?若能,请你写出求解过程;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】D是△ABC内一点,那么,在下列结论中错误的是( ).
A. BD+CD>BCB. ∠BDC>∠AC. BD>CDD. AB+AC>BD+CD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在以线段AB为直径的⊙O上取一点,连接AC、BC.将△ABC沿AB翻折后得到△ABD.

(1)试说明点D在⊙O上;
(2)在线段AD的延长线上取一点E,使AB2=AC·AE.求证:BE为⊙O的切线;
(3)在(2)的条件下,分别延长线段AE、CB相交于点F,若BC=2,AC=4,求线段EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是某同学对多项式(x2-2x)(x2-2x+2)+1进行因式分解的过程:
解:设x2-2x=y
原式=y (y+2)+1 (第一步)
=y2+2y+1 (第二步)
=(y+1)2 (第三步)
=(x2-2x+1)2 (第四步)
请问:
(1)该同学因式分解的结果是否彻底? (填“彻底”或“不彻底”),若不彻底,则该因式分解的最终结果为 ;
(2)请你模仿上述方法,对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)(发现)如图①,已知等边△ABC,将直角三角板的60°角顶点D任意放在BC边上(点D不与点B、C重合),使两边分别交线段AB、AC于点E、F.
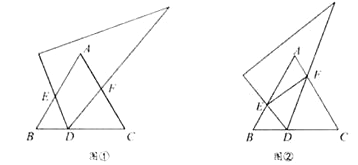
①若AB=6,AE=4,BD=2,则CF =________;
②求证:△EBD∽△DCF.
(2)(思考)若将图①中的三角板的顶点D在BC边上移动,保持三角板与边AB、AC的两个交点E、F都存在,连接EF,如图②所示.问点D是否存在某一位置,使ED平分∠BEF且FD平分∠CFE?若存在,求出
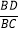 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(3)(探索)如图③,在等腰△ABC中,AB=AC,点O为BC边的中点,将三角形透明纸板的一个顶点放在点O处(其中∠MON=∠B),使两条边分别交边AB、AC于点E、F(点E、F均不与△ABC的顶点重合),连接EF.设∠B=α,则△AEF与△ABC的周长之比为________(用含α的表达式表示)
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“五一”期间,部分同学随家长一同到某公园游玩,下面是购买门票时,甲同学与其爸爸的对话(如图),试根据图中的信息,解决下列问题:
(1)本次共去了几个成人,几个学生?
(2)甲同学所说的另一种购票方式,是否可以省钱?试说明理由.

相关试题

