【题目】如图①,在平面直角坐标系xOy 中,抛物线y=ax2+bx+3经过点A(-1,0) 、B(3,0) 两点,且与y轴交于点C
.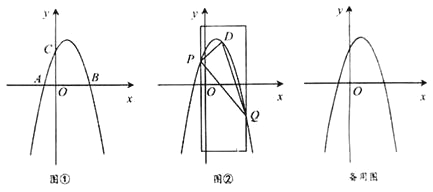
(1)求抛物线的表达式;
(2)如图②,用宽为4个单位长度的直尺垂直于x轴,并沿x轴左右平移,直尺的左右两边所在的直线与抛物线相交于P、 Q两点(点P在点Q的左侧),连接PQ,在线段PQ上方抛物线上有一动点D,连接DP、DQ.
①若点P的横坐标为![]() ,求△DPQ面积的最大值,并求此时点D 的坐标;
,求△DPQ面积的最大值,并求此时点D 的坐标;
②直尺在平移过程中,△DPQ面积是否有最大值?若有,求出面积的最大值;若没有,请说明理由.
参考答案:
【答案】(1)抛物线y=-x2+2x+3;(2)①点D( ![]() );②△PQD面积的最大值为8
);②△PQD面积的最大值为8
【解析】(1)根据点A、B的坐标,利用待定系数法即可求出抛物线的表达式;
(2)(I)由点P的横坐标可得出点P、Q的坐标,利用待定系数法可求出直线PQ的表达式,过点D作DE∥y轴交直线PQ于点E,设点D的坐标为(x,-x2+2x+3),则点E的坐标为(x,-x+![]() ),进而即可得出DE的长度,利用三角形的面积公式可得出S△DPQ=-2x2+6x+
),进而即可得出DE的长度,利用三角形的面积公式可得出S△DPQ=-2x2+6x+![]() ,再利用二次函数的性质即可解决最值问题;
,再利用二次函数的性质即可解决最值问题;
(II)假设存在,设点P的横坐标为t,则点Q的横坐标为4+t,进而可得出点P、Q的坐标,利用待定系数法可求出直线PQ的表达式,设点D的坐标为(x,-x2+2x+3),则点E的坐标为(x,-2(t+1)x+t2+4t+3),进而即可得出DE的长度,利用三角形的面积公式可得出S△DPQ=-2x2+4(t+2)x-2t2-8t,再利用二次函数的性质即可解决最值问题.
(1)将A(-1,0)、B(3,0)代入y=ax2+bx+3,得:
![]() ,解得:
,解得:![]() ,
,
∴抛物线的表达式为y=-x2+2x+3.
(2)(I)当点P的横坐标为-![]() 时,点Q的横坐标为
时,点Q的横坐标为![]() ,
,
∴此时点P的坐标为(-![]() ,
,![]() ),点Q的坐标为(
),点Q的坐标为(![]() ,-
,-![]() ).
).
设直线PQ的表达式为y=mx+n,
将P(-![]() ,
,![]() )、Q(
)、Q(![]() ,-
,-![]() )代入y=mx+n,得:
)代入y=mx+n,得:
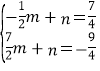 ,解得:
,解得: ,
,
∴直线PQ的表达式为y=-x+![]() .
.
如图②,过点D作DE∥y轴交直线PQ于点E,

设点D的坐标为(x,-x2+2x+3),则点E的坐标为(x,-x+![]() ),
),
∴DE=-x2+2x+3-(-x+![]() )=-x2+3x+
)=-x2+3x+![]() ,
,
∴S△DPQ=![]() DE(xQ-xP)=-2x2+6x+
DE(xQ-xP)=-2x2+6x+![]() =-2(x-
=-2(x-![]() )2+8.
)2+8.
∵-2<0,
∴当x=![]() 时,△DPQ的面积取最大值,最大值为8,此时点D的坐标为(
时,△DPQ的面积取最大值,最大值为8,此时点D的坐标为(![]() ,
,![]() ).
).
(II)假设存在,设点P的横坐标为t,则点Q的横坐标为4+t,
∴点P的坐标为(t,-t2+2t+3),点Q的坐标为(4+t,-(4+t)2+2(4+t)+3),
利用待定系数法易知,直线PQ的表达式为y=-2(t+1)x+t2+4t+3.
设点D的坐标为(x,-x2+2x+3),则点E的坐标为(x,-2(t+1)x+t2+4t+3),
∴DE=-x2+2x+3-[-2(t+1)x+t2+4t+3]=-x2+2(t+2)x-t2-4t,
∴S△DPQ=![]() DE(xQ-xP)=-2x2+4(t+2)x-2t2-8t=-2[x-(t+2)]2+8.
DE(xQ-xP)=-2x2+4(t+2)x-2t2-8t=-2[x-(t+2)]2+8.
∵-2<0,
∴当x=t+2时,△DPQ的面积取最大值,最大值为8.
∴假设成立,即直尺在平移过程中,△DPQ面积有最大值,面积的最大值为8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“五一”期间,部分同学随家长一同到某公园游玩,下面是购买门票时,甲同学与其爸爸的对话(如图),试根据图中的信息,解决下列问题:
(1)本次共去了几个成人,几个学生?
(2)甲同学所说的另一种购票方式,是否可以省钱?试说明理由.

-
科目: 来源: 题型:
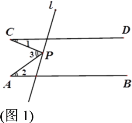
查看答案和解析>>【题目】已知直线AB∥CD,点P为直线l上一点,尝试探究并解答:
(1)如图1,若点P在两平行线之间,∠1=23°,∠2=35°,则∠3= ;
(2)探究图1中∠1,∠2与∠3之间的数量关系,并说明理由;
(3)如图2,若点P在CD的上方,探究∠1,∠2与∠3之间有怎样的数量关系,并说明理由;
(4)如图3,若∠PCD与∠PAB的平分线交于点P1,∠DCP1与∠BAP1的平分线交于点P2,∠DCP2与∠BAP2的平分线交于点P3,…,∠DCPn-1与∠BAPn-1的平分线交于点Pn,若∠PCD=α,∠PAB=β,直接写出∠APnC的度数(用含α与β的代数式表示).


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,D,E分别为AB,AC上一点,将△BCD,△ADE分别沿CD,DE折叠,点A、B恰好重合于点A'处.若∠A'CA=18°,则∠A=____°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学课本中,有这样一道题:已知:如(图1),∠B+∠C=∠BEC求证:AB∥CD
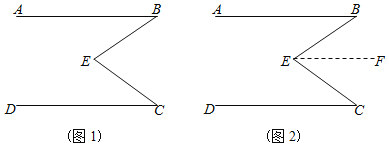
(1)请补充下面证明过程
证明:过点E,做EF∥AB,如(图2)
∴∠B=∠
∵∠B+∠C=∠BEC∠BEF+∠FEC=∠BEC(已知)
∴∠B+∠C=∠BEF+∠FEC(等量代换)
∴∠ =∠ (等式性质)
∴EF∥
∵EF∥AB
∴AB∥CD(平行于同一条直线的两条直线互相平行)
(2)请再选用一种方法,加以证明
-
科目: 来源: 题型:
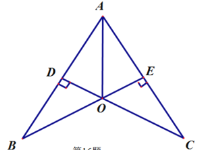
查看答案和解析>>【题目】如图,已知CD⊥AB于点D,BE⊥ AC于点E, CD、 BE交于点O,且AO平分∠BAC,则图中的全等三角形共有_________________对。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
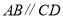 ,
,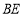 平分
平分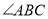 ,
,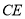 平分
平分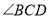 ,点
,点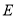 在
在 上,求证:
上,求证: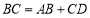 .
.
相关试题

