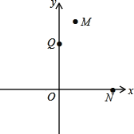
【题目】已知,在平面直角坐标系中,点M、N的坐标分别为(1,4)和(3,0),点Q是y轴上的一个动点,且M、N、Q三点不在同一直线上,当△MNQ的周长最小时,则点Q的坐标是___.
参考答案:
【答案】(0,3).
【解析】
根据平面直角坐标系找出N关于y轴的对称点N′位置,连接MN′,根据轴对称确定最短路线问题交点即为△MNQ的周长最小的点Q的位置,根据MD和N′D确定△MDN′是等腰直角三角形,进而求得△QON′是等腰直角三角形,即可求得OQ的长.
作点N关于y轴的对称点N′,连接MN′交y轴于点Q,
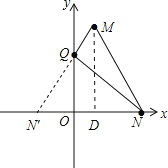
则此时△MNQ的周长最小,
理由:∵点N的坐标是(3,0),
∴点N′的坐标是(-3,0),
过点M作MD⊥x轴,垂足为点D
∵点M的坐标是(1,4)
∴N′D=MD=4
∴∠MN′D=45°,
∴N′O=OQ=3,
即点Q的坐标是(0,3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面的图像反映的过程是:小明从家去超市买文具,又去书店购书,然后回家.其中x表示时间,y表示小明离他家的距离,若小明家、超市、书店在同一条直线上.
根据图像回答下列问题:

(1)超市离小明家多远,小明走到超市用了多少时间?
(2)超市离书店多远,小明在书店购书用了多少时间?
(3)书店离小明家多远,小明从书店走回家的平均速度是每分钟多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数
 的图象上,从左向右第3个正方形中的一个顶点A的坐标为
的图象上,从左向右第3个正方形中的一个顶点A的坐标为 ,阴影三角形部分的面积从左向右依次记为
,阴影三角形部分的面积从左向右依次记为 、
、 、
、 、
、 、
、 ,则
,则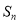 的值为______
的值为______ 用含n的代数式表示,n为正整数
用含n的代数式表示,n为正整数

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b为实数,下列说法:①若a,b互为相反数,则
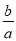 =﹣1;②若a+b<0,ab>0,则|2a+b|=﹣2a﹣b;③若|a|>|b|,则(a+b)(a﹣b)是正数;其中正确的有( )个.
=﹣1;②若a+b<0,ab>0,则|2a+b|=﹣2a﹣b;③若|a|>|b|,则(a+b)(a﹣b)是正数;其中正确的有( )个.A.0B.1C.2D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了让同学们了解自己的体育水平,初二 1 班的体育老师对全班 45 名学生进行了一次体育模拟测试(得分均为整数),成绩满分为 10 分,1 班的体育委员根据这次测试成绩,制作了统计图和分析表如下:
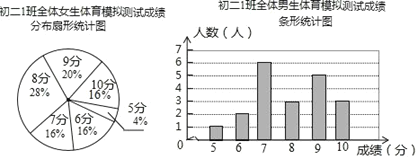
根据以上信息,解答下列问题
(1)这个班共有男生 人,共有女生 人;
(2)求初二 1 班女生体育成绩的众数是 ,男生体育成绩的中位数是 。
(3)若全年级有 630 名学生,体育测试 9 分及以上的成绩为 A 等,试估计全年级体育测试成绩达到 A 等的有多少名学生?
-
科目: 来源: 题型:
查看答案和解析>>【题目】重庆市的重大惠民工程--公租房建设已陆续竣工,计划10年内解决低收入人群的住房问题,前6年,每年竣工投入使用的公租房面积
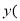 单位:百万平方米
单位:百万平方米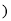 ,与时间x的关系是
,与时间x的关系是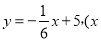 单位:年,
单位:年, 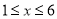 且x为整数
且x为整数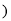 ;后4年,每年竣工投入使用的公租房面积
;后4年,每年竣工投入使用的公租房面积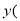 单位:百万平方米
单位:百万平方米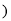 ,与时间x的关系是
,与时间x的关系是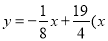 单位:年,
单位:年, 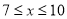 且x为整数
且x为整数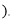 假设每年的公租房全部出租完
假设每年的公租房全部出租完 另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金
另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金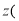 单位:元
单位:元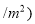 与时间
与时间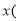 单位:年,
单位:年, 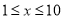 且x为整数
且x为整数 满足一次函数关系如下表:
满足一次函数关系如下表: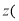 元
元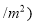
50
52
54
56
58

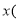 年
年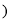
1
2
3
4
5

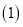 求出z与x的函数关系式;
求出z与x的函数关系式;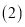 求政府在第几年投入的公租房收取的租金最多,最多为多少百万元;
求政府在第几年投入的公租房收取的租金最多,最多为多少百万元;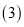 若第6年竣工投入使用的公租房可解决20万人的住房问题,政府计划在第10年投入的公租房总面积不变的情况下,要让人均住房面积比第6年人均住房面积提高
若第6年竣工投入使用的公租房可解决20万人的住房问题,政府计划在第10年投入的公租房总面积不变的情况下,要让人均住房面积比第6年人均住房面积提高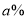 ,这样可解决住房的人数将比第6年减少
,这样可解决住房的人数将比第6年减少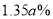 ,求a的值.
,求a的值. 参考数据:
参考数据: 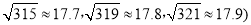
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是反比例函数
 (x>0)图象上的任意一点,过点A作AB∥x轴,交另一个反比例函数
(x>0)图象上的任意一点,过点A作AB∥x轴,交另一个反比例函数 (k<0,x<0)的图象于点B,且S△AOB=5.
(k<0,x<0)的图象于点B,且S△AOB=5.(1) k的值为_______;
(2) 若点A的横坐标是1,
①求∠AOB的度数;
②在y2的图象上找一点P(异于点B), 使S△AOP=S△AOB,求点P的坐标.

相关试题

