【题目】重庆市的重大惠民工程--公租房建设已陆续竣工,计划10年内解决低收入人群的住房问题,前6年,每年竣工投入使用的公租房面积![]() 单位:百万平方米
单位:百万平方米![]() ,与时间x的关系是
,与时间x的关系是![]() 单位:年,
单位:年, ![]() 且x为整数
且x为整数![]() ;后4年,每年竣工投入使用的公租房面积
;后4年,每年竣工投入使用的公租房面积![]() 单位:百万平方米
单位:百万平方米![]() ,与时间x的关系是
,与时间x的关系是![]() 单位:年,
单位:年, ![]() 且x为整数
且x为整数![]() 假设每年的公租房全部出租完
假设每年的公租房全部出租完![]() 另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金
另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金![]() 单位:元
单位:元![]() 与时间
与时间![]() 单位:年,
单位:年, ![]() 且x为整数
且x为整数![]() 满足一次函数关系如下表:
满足一次函数关系如下表:
| 50 | 52 | 54 | 56 | 58 |
|
| 1 | 2 | 3 | 4 | 5 |
|
![]() 求出z与x的函数关系式;
求出z与x的函数关系式;
![]() 求政府在第几年投入的公租房收取的租金最多,最多为多少百万元;
求政府在第几年投入的公租房收取的租金最多,最多为多少百万元;
![]() 若第6年竣工投入使用的公租房可解决20万人的住房问题,政府计划在第10年投入的公租房总面积不变的情况下,要让人均住房面积比第6年人均住房面积提高
若第6年竣工投入使用的公租房可解决20万人的住房问题,政府计划在第10年投入的公租房总面积不变的情况下,要让人均住房面积比第6年人均住房面积提高![]() ,这样可解决住房的人数将比第6年减少
,这样可解决住房的人数将比第6年减少![]() ,求a的值.
,求a的值.
![]() 参考数据:
参考数据: ![]()
参考答案:
【答案】(1) ![]() (2)第3年收取的租金最多,最多为243百万元;(3)a的值为20.
(2)第3年收取的租金最多,最多为243百万元;(3)a的值为20.
【解析】分析:
(1)根据表中所给数据,用待定系数法即可求得z与x间的函数关系式;
(2)设收取的租金为w百万元,由题意可知![]() ,然后分
,然后分![]() 和
和![]() 两种情况把y和z关于x的表达式代入
两种情况把y和z关于x的表达式代入![]() 中得到w与x间的函数关系式得到各自的最大值,进行比较即可得到本题答案了;
中得到w与x间的函数关系式得到各自的最大值,进行比较即可得到本题答案了;
(3)由题意分别计算出第6年和第10年竣工投入使用的公租房面积,然后根据题意列出关于a%的方程,解方程即可求得a的值.
详解:
![]() 由题意,z与x是一次函数关系,设
由题意,z与x是一次函数关系,设![]()
把![]() 代入,得
代入,得
![]() ,
,
![]() .
.
![]() 当
当![]() 时,设收取的租金为
时,设收取的租金为![]() 百万元,则
百万元,则
![]()
∵对称轴![]() ,且
,且![]() ,
,
∴当![]() 时,
时, ![]() 最大
最大![]() 百万元
百万元![]()
当![]() 时,设收取的租金为
时,设收取的租金为![]() 百万元,则
百万元,则
![]()
∵对称轴![]()
∴当![]() 时,
时, ![]() 最大
最大![]() 百万元
百万元![]()
∵![]()
∴第3年收取的租金最多,最多为243百万元.
![]() 当
当![]() 时,
时, ![]() 百万平方米
百万平方米![]() 万平方米
万平方米
当![]() 时,
时, ![]() 百万平方米
百万平方米![]() 万平方米
万平方米
∵第6年可解决20万人住房问题,
∴人均住房为: ![]() 平方米.
平方米.
由题意: ![]() ,
,
设![]() ,化简为:
,化简为:![]() ,
,
![]() ,
,
∴![]()
∵![]() ,
,
∴![]() 不符题意,舍去
不符题意,舍去![]() ,
,
∴![]() ,
,
∴![]()
答:a的值为20.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b为实数,下列说法:①若a,b互为相反数,则
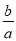 =﹣1;②若a+b<0,ab>0,则|2a+b|=﹣2a﹣b;③若|a|>|b|,则(a+b)(a﹣b)是正数;其中正确的有( )个.
=﹣1;②若a+b<0,ab>0,则|2a+b|=﹣2a﹣b;③若|a|>|b|,则(a+b)(a﹣b)是正数;其中正确的有( )个.A.0B.1C.2D.3
-
科目: 来源: 题型:
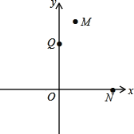
查看答案和解析>>【题目】已知,在平面直角坐标系中,点M、N的坐标分别为(1,4)和(3,0),点Q是y轴上的一个动点,且M、N、Q三点不在同一直线上,当△MNQ的周长最小时,则点Q的坐标是___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了让同学们了解自己的体育水平,初二 1 班的体育老师对全班 45 名学生进行了一次体育模拟测试(得分均为整数),成绩满分为 10 分,1 班的体育委员根据这次测试成绩,制作了统计图和分析表如下:
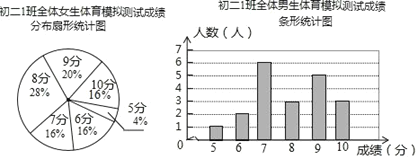
根据以上信息,解答下列问题
(1)这个班共有男生 人,共有女生 人;
(2)求初二 1 班女生体育成绩的众数是 ,男生体育成绩的中位数是 。
(3)若全年级有 630 名学生,体育测试 9 分及以上的成绩为 A 等,试估计全年级体育测试成绩达到 A 等的有多少名学生?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是反比例函数
 (x>0)图象上的任意一点,过点A作AB∥x轴,交另一个反比例函数
(x>0)图象上的任意一点,过点A作AB∥x轴,交另一个反比例函数 (k<0,x<0)的图象于点B,且S△AOB=5.
(k<0,x<0)的图象于点B,且S△AOB=5.(1) k的值为_______;
(2) 若点A的横坐标是1,
①求∠AOB的度数;
②在y2的图象上找一点P(异于点B), 使S△AOP=S△AOB,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明帮助小芳荡秋千(如图1),在小明的助推下,秋千越来越高,秋千离地面的高度
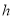 (
(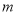 )与摆动时间
)与摆动时间 (
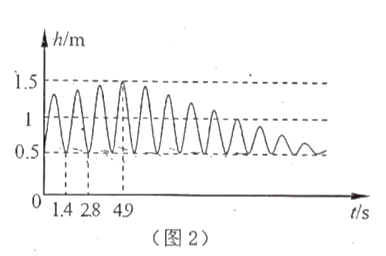
(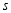 )之间的关系如图2所示.
)之间的关系如图2所示.(1)根据函数定义,请判断变量
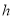 是否为关于
是否为关于 的函数?
的函数?(2)结合图象回答:
①秋千静止时离地面的距离是多少?秋千的最高点与地面距离是多少?
②多长时间后小明就不再推小芳?
③从最低点开始向前和向后,再反悔到最低点,这叫做一个周期,请问,小芳完成第一个周期用了多长时间?
④每个周期的时间都是相等的,经过多长时间,秋千的最高点是1m?

-
科目: 来源: 题型:
查看答案和解析>>【题目】中国经济的快速发展让众多国家感受到了威胁,随着钓鱼岛事件、南海危机、萨德入韩等一系列事件的发生,国家安全一再受到威胁,所谓“国家兴亡,匹夫有责”,某校积极开展国防知识教育,九年级甲、乙两班分别选5名同学参加“国防知识”比赛,其预赛成绩如图所示:
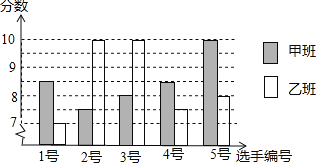
 根据上图填写下表:
根据上图填写下表:平均数
中位数
众数
方差
甲班
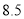

______
______
乙班

______
10

 根据上表数据,分别从平均数、中位数、众数、方差的角度分析哪个班的成绩较好.
根据上表数据,分别从平均数、中位数、众数、方差的角度分析哪个班的成绩较好.
相关试题

