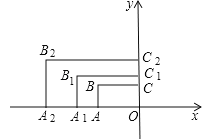
【题目】如图,在平面直角坐标系中,矩形AOCB的两边OA、OC分别在x轴和y轴上,且OA=2,OC=1.在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的![]() 倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大
倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大![]() 倍,得到矩形A2OC2B2…,以此类推,得到的矩形AnOCnBn的对角线交点的坐标为 .
倍,得到矩形A2OC2B2…,以此类推,得到的矩形AnOCnBn的对角线交点的坐标为 .
参考答案:
【答案】(﹣![]() ,
,![]() ).
).
【解析】
试题分析:∵在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的![]() 倍,∴矩形A1OC1B1与矩形AOCB是位似图形,点B与点B1是对应点,∵OA=2,OC=1.
倍,∴矩形A1OC1B1与矩形AOCB是位似图形,点B与点B1是对应点,∵OA=2,OC=1.
∵点B的坐标为(﹣2,1),∴点B1的坐标为(﹣2×![]() ,1×
,1×![]() ),∵将矩形A1OC1B1以原点O为位似中心放大
),∵将矩形A1OC1B1以原点O为位似中心放大![]() 倍,得到矩形A2OC2B2…,∴B2(﹣2×
倍,得到矩形A2OC2B2…,∴B2(﹣2×![]() ×
×![]() ,1×
,1×![]() ×
×![]() ),∴Bn(﹣2×
),∴Bn(﹣2×![]() ,1×
,1×![]() ),∵矩形AnOCnBn的对角线交点(﹣2×
),∵矩形AnOCnBn的对角线交点(﹣2×![]() ×
×![]() ,1×
,1×![]() ×
×![]() ),即(﹣
),即(﹣![]() ,
,![]() ),故答案为:(﹣
),故答案为:(﹣![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a与b互为相反数,c与d互为倒数,则(a+b)2016﹣3(cd)2017= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,三角形ABC(记作△ABC)在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是A(﹣2,1),B(﹣3,﹣2),C(1,﹣2),先将△ABC向上平移3个单位长度,再向右平移2个单位长度,得到A1B1C1 .

(1)在图中画出△A1B1C1;
(2)点A1 , B1 , C1的坐标分别为、、;
(3)若y轴有一点P,使△PBC与△ABC面积相等,求出P点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,是真命题的是( )
A.平分弦的直径垂直于弦B.圆内接平行四边形必为矩形
C.任意三个点确定一个圆D.相等圆心角所对的弧相等
-
科目: 来源: 题型:
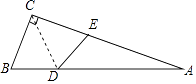
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处,若∠A=25°,则∠ADE的度数为( )
A.20°
B.30°
C.40°
D.50° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )
A. 选①② B. 选选①③ C. 选②③ D. 选②④
-
科目: 来源: 题型:
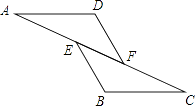
查看答案和解析>>【题目】如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )
A.∠A=∠C
B.AD=CB
C.BE=DF
D.AD∥BC
相关试题

