搜索
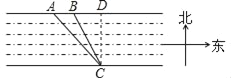
【题目】在一次数学活动课上，老师带领学生去测长江的宽度，某学生在长江北岸点A处观测到长江对岸水边有一点C，测得C在A东南方向上，沿长江边向东前行200米到达B处，测得C在B南偏东30°的方向上．
（1）画出学生测量的示意图；
（2）请你根据以上数据，帮助该同学计算出长江的宽度（精确到0.1 m）．
参考答案：
【答案】（1）测量的示意图见解析；（2）x≈473.2米．
【解析】试题分析：(1)、根据题中给出的角度问题得出点A、B、C、D的四个位置，从而画出图形；(2)、设CD=x米，根据等腰三角形的性质得出AD=x米，根据Rt△CBD的性质得出BD=
x米，最后根据AB=AD-BD=200求出x的值．
试题解析：解：(1)、测量的示意图如右图；
(2)、设长江的宽度CD为x米，∵直角三角形ACD中，∠ACD=45°， ∴AD=CD=x
∵直角三角形CBD中，∠BCD=30°， BD=CDtan30°=
x，AB=200，
∴x﹣x=200， 则x≈473.2（米）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，∠ACB＝90°，sinA＝
，BC＝8，点D是AB的中点，过点B作CD的垂线，垂足为点E.(1)求线段CD的长；
(2)求cos∠ABE的值。
-
科目： 来源： 题型：
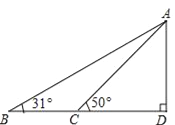
查看答案和解析>>【题目】据调查，超速行驶是引发交通事故的主要原因之一，所以规定以下情境中的速度不得超过15m/s，在一条笔直公路BD的上方A处有一探测仪，如图，AD=24m，∠D=90°，第一次探测到一辆轿车从B点匀速向D点行驶，测得∠ABD=31°，2秒后到达C点，测得∠ACD=50°.
（1）求B，C的距离．
（2）通过计算，判断此轿车是否超速．（tan31°≈0.6，tan50°≈1.2，结果精确到1m）
-
科目： 来源： 题型：
查看答案和解析>>【题目】某中学为了了解七年级男生入学时的跳绳情况，随机选取50名刚入学的男生进行个人一分钟跳绳测试，并以测试数据为样本，绘制出部分频数分布表和部分频数分布直方图（如图所示）．根据图表解答下列问题：
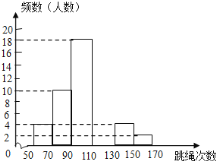
（1）a= ，b= ；
（2）这个样本数据的中位数落在第 组；
（3）若七年级男生个人一分钟跳绳次数x≥130时成绩为优秀，则从这50名男生中任意选一人，跳绳成绩为优秀的概率为多少；
（4）若该校七年级入学时男生共有150人，请估计此时该校七年级男生个人一分钟跳绳成绩为优秀的人数．
组别
次数x
频数（人数）
第1组
50≤x＜70
4
第2组
70≤x＜90
a
第3组
90≤x＜110
18
第4组
110≤x＜130
b
第5组
130≤x＜150
4
第6组
150≤x＜170
2
-
科目： 来源： 题型：
查看答案和解析>>【题目】在0，3.14，
，2π，－
，
，－0.4，－
，4.262262226…(每两个”6”之间依次多一个”2”)中，属于有理数的有_________________________________________________；
属于无理数的有________________________________________________________；
属于正实数的有_________________________________________________________；
属于负实数的有_____________________________________________________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】两块完全相同的三角板Ⅰ（△ABC）和Ⅱ（△A1B1C1）如图①放置在同一平面上（∠C=∠C1=90°，∠ABC=∠A1B1C1=60°），斜边重合．若三角板Ⅱ不动，三角板Ⅰ在三角板Ⅱ所在的平面上向右滑动，图②是滑动过程中的一个位置．
（1）在图②中，连接BC1、B1C，求证：△A1BC1≌△AB1C；
（2）三角板Ⅰ滑到什么位置（点B1落在AB边的什么位置）时，四边形BCB1C1是菱形？说明理由．
-
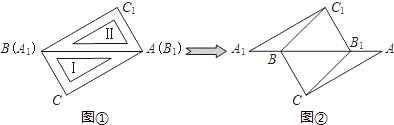
科目： 来源： 题型：
查看答案和解析>>【题目】用适当的方法解下列方程：
（1）（x﹣1）2=9
（2）3x2﹣6x=0
（3）x2+2x=5
（4）4x2﹣8x+1=0（用公式法）
相关试题
