【题目】如图,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角平分线CF于点F.

(1)求证:AE=EF;
(2)如图2,若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”,其余条件不变,(1)中的结论是否仍然成立? ;(填“成立”或“不成立”);
(3)如图3,若把条件“点E是边BC的中点”改为“点E是边BC延长线上的一点”,其余条件仍不变,那么结论AE=EF是否成立呢?若成立请证明,若不成立说明理由.
参考答案:
【答案】(1)证明见解析;(2)成立;(3)成立,证明见解析.
【解析】试题分析:(1)取AB中点M,连接EM,求出BM=BE,得出∠BME=45°,求出∠AME=∠ECF=135°,求出∠MAE=∠FEC,根据ASA推出△AME和△ECF全等即可;
(2)截取BE=BM,连接EM,求出AM=EC,得出∠BME=45°,求出∠AME=∠ECF=135°,求出∠MAE=∠FEC,根据ASA推出△AME和△ECF全等即可;
(3)在BA的延长线上取一点N,使AN=CE,连接NE,根据已知利用ASA判定△ANE≌△ECF,因为全等三角形的对应边相等,所以AE=EF.
试题解析:(1)证明:取AB中点M,连接EM,

∵AB=BC,E为BC中点,M为AB中点,
∴AM=CE=BE,
∴∠BME=∠BME=45°,
∴∠AME=135°=∠ECF,
∵∠B=90°,
∴∠BAE+∠AEB=90°,
∵∠AEF=90°,
∴∠AEB+∠FEC=90°,
∴∠BAE=∠FEC,
在△AME和△ECF中, 
∴△AME≌△ECF(ASA),
∴AE=EF;
(2)成立,
理由是:如图,在AB上截取BM=BE,连接ME,

∵∠B=90°,
∴∠BME=∠BEM=45°,
∴∠AME=135°=∠ECF,
∵AB=BC,BM=BE,
∴AM=EC,
在△AME和△ECF中, 
∴△AME≌△ECF(ASA),
∴AE=EF;
(3)成立.
证明:如图,在BA的延长线上取一点N.使AN=CE,连接NE,

∴BN=BE,
∴∠N=∠NEC=45°,
∵CF平分∠DCG,
∴∠FCE=45°,
∴∠N=∠ECF,
∵四边形ABCD是正方形,
∴AD∥BE,
∴∠DAE=∠BEA,即∠DAE+90°=∠BEA+90°,
∴∠NAE=∠CEF,
∴△ANE≌△ECF(ASA),
∴AE=EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的周长为16 cm,∠BAD=120°对角线AC,BD相交于点O,过点O作BC的垂线交BC于点E,交AD于点F,求EF长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,正六边形ABCDEF在直角坐标系的位置如图所示,A(﹣2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过5次翻转之后,点B的坐标是______.

-
科目: 来源: 题型:
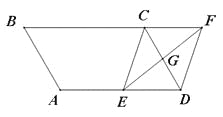
查看答案和解析>>【题目】(7分)如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)①当AE= cm时,四边形CEDF是矩形;
②当AE= cm时,四边形CEDF是菱形;(直接写出答案,不需要说明理由)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)将一张长方形纸条ABCD按如图所示折叠,若折叠角∠FEC=64°.
(1)求∠1的度数;
(2)求证:△EFG是等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=2
 x2的图象如图所示,点O为坐标原点,点A在y轴的正半轴上,点B、C在函数图象上,四边形OBAC为菱形,且∠OBA=120°,则点C的坐标为______.
x2的图象如图所示,点O为坐标原点,点A在y轴的正半轴上,点B、C在函数图象上,四边形OBAC为菱形,且∠OBA=120°,则点C的坐标为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果店老板用400元购进一批葡萄,由于葡萄新鲜很快售完,老板又用500元购进第二批葡萄,所购数量与第一批相同,但每千克进价比第一批贵2元.
(1)求第一批葡萄进价为每千克多少元;
(2)若老板以每千克11元的价格将两批葡萄全部售完,可以盈利多少元.
相关试题

