【题目】已知关于x的方程x2-(k+2)x+2k=0.
(1)求证:k取任何实数值,方程总有实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长.
参考答案:
【答案】
(1)证明:∵△=b2﹣4ac=(k+2)2﹣8k=(k﹣2)2≥0,∴无论k取任意实数值,方程总有实数根;
(2)解:把x=1代入x2-(k+2)x+2k=0中,1-(k+2)+2k=0,k=1,
把k=1代入x2-(k+2)x+2k=0中,
x=1或x=2,
所以方程的另一根是2.
①当1,2为直角边时,斜边为 ![]()
此时直角三角形周长为 ![]()
②当2为斜边,1为直角边时,另一直角边为 ![]()
此时直角三角形周长为 ![]()
综上所述,直角三角形的周长为 ![]() .
.
【解析】(1)首先算出此方程的△=b2﹣4ac=(k+2)2﹣8k=(k﹣2)2,根据平方的非负性得出≥0,从而得出结论k取任何实数值,方程总有实数根;
(2)根据方程根的定义把把x=1代入x2-(k+2)x+2k=0中 ,得出一个关于k的一元一次方程,解方程得出k的值,从而把k=1代入x2-(k+2)x+2k=0中,得出一个关于x的方程,解方程得出方程的另一个根;然后分类讨论:①当1,2为直角边时,根据勾股定理得出斜边的长,从而算出直角三角形的周长;②当2为斜边,1为直角边时,根据勾股定理算出另一直角边的长,从而算出直角三角形的周长 ;综上所述,得出结论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.

(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F

(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示是几种名车的标志,请指出:这几个图案中轴对称图形有( )

A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】过四边形的一个顶点可以画一条对角线,且把四边形分成两个三角形;过五边形的一个顶点可以画两条对角线,且把五边形分成三个三角形;......猜想:过n边形的一个顶点可以画_________条对角线,且把n边形分成 _________个三角形.
-
科目: 来源: 题型:
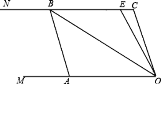
查看答案和解析>>【题目】如图,已知两条射线OM∥CN,动线段AB的两个端点A,B分别在射线OM,CN上,且∠C=∠OAB=108°,点E在线段CB上,OB平分∠AOE.
(1)图中有哪些与∠AOC相等的角?并说明理由;
(2)若平移AB,那么∠OBC与∠OEC的度数比是否随着AB位置变化而变化?若变化,找出变化规律;若不变,求出这个比值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,CE平分∠ACB,交AB于点E.

(1)求证:AC平分∠DAB;
(2)求证:△PCE是等腰三角形.
相关试题

