【题目】如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.

(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
参考答案:
【答案】解:(1)证明:∵D、E分别是AB、AC的中点,∴DE∥BC且2DE=BC。
又∵BE=2DE,EF=BE,∴EF=BC,EF∥BC。
∴四边形BCFE是平行四边形。
又∵BE=FE,∴四边形BCFE是菱形。
(2)∵∠BCF=120°,∴∠EBC=60°。
∴△EBC是等边三角形。
∴菱形的边长为4,高为![]() 。
。
∴菱形的面积为4×![]() =
=![]() 。
。
【解析】
试题(1)从所给的条件可知,DE是△ABC中位线,所以DE∥BC且2DE=BC,所以BC和EF平行且相等,所以四边形BCFE是平行四边形,又因为BE=FE,所以四边形BCFE是菱形。
(2)因为∠BCF=120°,所以∠EBC=60°,所以菱形的边长也为4,求出菱形的高面积就可求。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABO的面积为8,OA=OB,BC=12,点P的坐标是(a,6).
(1) △ABC三个顶点的坐标分别为A( , ),B( , ),C( , );
(2) 是否存在点P,使得
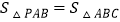 ?若存在,求出满足条件的所有点P的坐标.
?若存在,求出满足条件的所有点P的坐标. 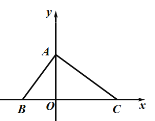
-
科目: 来源: 题型:
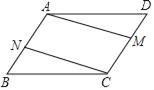
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥CD,AD∥BC,AN=CM.
(1)求证:BN=DM;
(2)若BC=3,CD=2,∠B=50°,求∠BCD、∠D的度数及四边形ABCD的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向C处,某一时刻,AC=18
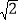 km,且OA=OC.轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为40km/h和30km/h,经过0.2h,轮船甲行驶至B处,轮船乙行驶至D处,求此时B处距离D处多远?
km,且OA=OC.轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为40km/h和30km/h,经过0.2h,轮船甲行驶至B处,轮船乙行驶至D处,求此时B处距离D处多远?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F

(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示是几种名车的标志,请指出:这几个图案中轴对称图形有( )

A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2-(k+2)x+2k=0.
(1)求证:k取任何实数值,方程总有实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长.
相关试题

