【题目】如图,已知:长江路西段与黄河路的夹角为150°,长江路东段与淮河路的夹角为135°,黄河路全长AC=20km,从A地道B地必须先走黄河路经C点后再走淮河路才能到达,城市道路改造后,直接打通长江路(即修建AB路段).问:打通长江路后从A地道B地可少走多少路程?(参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7)
≈1.7)
参考答案:
【答案】解:如图所示:过点C作CD⊥AB于点D, 
在Rt△ACD中,∠CAD=30°,AC=20km,
则CD=10km,AD=10 ![]() km,
km,
在Rt△BCD中,∠CBD=45°,CD=10km,
故BD=10km,BC=10 ![]() km,
km,
则AC+BC﹣AB=20+10 ![]() ﹣10
﹣10 ![]() ﹣10≈7(km),
﹣10≈7(km),
答:打通长江路后从A地道B地可少走7km的路程.
【解析】首先过点C作CD⊥AB,垂足为D,首先依据含30°直角三角形的性质求得CD的长,然后再利用特殊锐角三角函数可求得AD的长,接下来,证明△CDB为等腰直角三角形,从而可求得BC、DB的长,最后,依据AC+BC﹣AB求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示是某班学生体重的频数分布直方图,则该班学生体重在40~45千克这一组的有________人,体重不足40千克的有________人.(注:40~45千克包括40千克,不包括45千克,其他同)
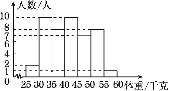
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,点
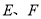 分别是
分别是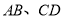 上的点,
上的点,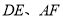 分别交
分别交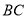 于
于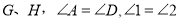 ,试说明
,试说明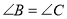 .阅读下面的解题过程,在横线上补全推理过程或依据.
.阅读下面的解题过程,在横线上补全推理过程或依据.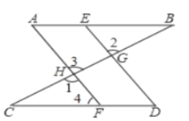
解:
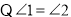 (已知)
(已知)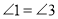 (______________________)
(______________________)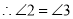 (等量代换)
(等量代换)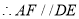 (_____________________)
(_____________________)∴
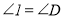 (__________________________)
(__________________________)又
 (已知)
(已知)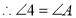 (等量代换)
(等量代换) ______(____________________________)
______(____________________________)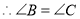 (_________________________)
(_________________________) -
科目: 来源: 题型:
查看答案和解析>>【题目】为了进一步了解八年级学生的身体素质情况,体育老师对八年级(1)班50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出不完整的频数分布表和频数分布直方图(如图).
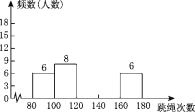
组别
次数(x)
频数(人数)
第1组
80≤x<100
6
第2组
100≤x<120
8
第3组
120≤x<140
a
第4组
140≤x<160
18
第5组
160≤x<180
6
请结合图表完成下列问题:
(1)表中的a=________;
(2)请把频数分布直方图补充完整;
(3)若规定:x<120为不合格;120≤x<140为合格;140≤x<160为良;x≥160为优.根据以上信息,请你给学校或八年级同学提一条合理化建议.
-
科目: 来源: 题型:
查看答案和解析>>【题目】眉山市三苏雕像广场是为了纪念三苏父子而修建的.原是一块长为(4a+2b)米,宽为(3a-b)米的长方形地块,现在政府对广场进行改造,计划将如图四周阴影部分进行绿化,中间将保留边长为(a+b)米的正方形三苏父子雕像,则绿化的面积是多少平方米?并求出当a=20,b=10时的绿化面积.
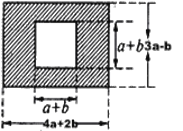
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣(x﹣1)2+c与x轴交于A,B(A,B分别在y轴的左右两侧)两点,与y轴的正半轴交于点C,顶点为D,已知A(﹣1,0).
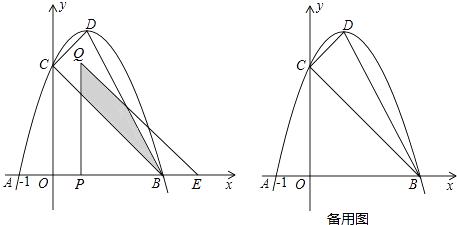
(1)求点B,C的坐标;
(2)判断△CDB的形状并说明理由;
(3)将△COB沿x轴向右平移t个单位长度(0<t<3)得到△QPE.△QPE与△CDB重叠部分(如图中阴影部分)面积为S,求S与t的函数关系式,并写出自变量t的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B两地相距4km,上午8:00时,亮亮从A地步行到B地,8:20时芳芳从B地出发骑自行车到A地,亮亮和芳芳两人离A地的距离S(km)与亮亮所用时间t(min)之间的函数关系如图所示,芳芳到达A地时间为( )
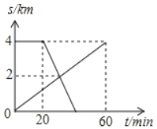
A. 8:30 B. 8:35 C. 8:40 D. 8:45
相关试题

