【题目】已知点![]() ,
,![]() 在直线
在直线![]() 的同侧,且
的同侧,且![]() 于
于![]() ,
,![]() 于
于![]() ,
,![]() ,
,![]() ,
,![]() ,现有点
,现有点![]() 在直线
在直线![]() 上,并且满足
上,并且满足![]() 与
与![]() 相似,则这样的点
相似,则这样的点![]() 的个数为( )
的个数为( )
A. 3 B. 5 C. 6 D. 7
参考答案:
【答案】C
【解析】
设DP=x,根据已知可以分三种情况:①当点P在线段BD上时;②当点P在线段BD的右侧时;③当点P在线段BD的左侧时;分别得出比例式得出方程,解方程求出x的值,即可得出结果.
∵AB⊥DB,CD⊥DB,
∴![]()
设DP=x,分三种情况:
当点P在线段BD上时,
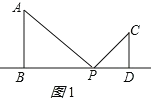
当PD:AB=CD:PB时,△PDC∽△ABP,
∴![]() 解得:DP=2或12,
解得:DP=2或12,
当PD:PB=CD:AB时,△PCD∽△PAB,
∴![]()
解得:DP=5.6;
当点P在线段BD的右侧,如图所示:
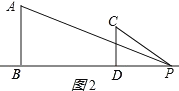
当PD:PB=CD:AB时,△PCD∽△PAB,
即![]()
解得:x=28;
当PD:AB=CD:PB时,△PCD∽△APB,
即![]()
解得:![]() (负值舍去),
(负值舍去),
∴![]()
当点P在线段BD的左侧时,如图所示:
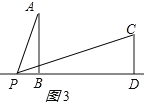
当PB:CD=AB:PD时,△PCD∽△APB,
即![]()
解得:![]() (负值舍去),
(负值舍去),
∴![]()
综上所述:当DP=5.6或2或12或28或![]() 或
或![]() 时,△ABP与△CDP相似,即这样的点P的个数有6个;
时,△ABP与△CDP相似,即这样的点P的个数有6个;
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列一段文字,再回答后面的问题.
已知在平面内两点P1(x1,y1),P2(x2,y2),这两点间的距离P1P2=
 ,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.
,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.(1)已知A(3,3),B(﹣2,﹣1),试求A,B两点间的距离;
(2)已知A,B在平行于y轴的直线上,点A的纵坐标为7,点B的纵坐标为﹣2,试求A,B两点间的距离;
(3)已知一个三角形各顶点坐标为A(0,5),B(﹣3,2),C(3,2),你能判断此三角形的形状吗?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与
与 轴仅有一个公共点
轴仅有一个公共点 ,经过点
,经过点 的直线交该抛物线于点
的直线交该抛物线于点 ,交
,交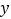 轴于点
轴于点 ,且点
,且点 是线段
是线段 的中点.
的中点.
 求这条抛物线对应的函数解析式;
求这条抛物线对应的函数解析式; 求直线
求直线 对应的函数解析式.
对应的函数解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)如图
 ,在平面直角坐标系
,在平面直角坐标系 中,抛物线
中,抛物线 经过点
经过点 ,顶点为点
,顶点为点 ,点
,点 为抛物线上的一个动点,
为抛物线上的一个动点, 是过点
是过点 且垂直于
且垂直于 轴的直线,过
轴的直线,过 作
作 ,垂足为
,垂足为 ,连接
,连接 .
. 求抛物线的解析式,并写出其顶点
求抛物线的解析式,并写出其顶点 的坐标;
的坐标; ①当
①当 点运动到
点运动到 点处时,计算:
点处时,计算: ________,
________, ________,由此发现,
________,由此发现, ________
________ (填“
(填“ ”、“
”、“ ”或“
”或“ ”);
”);②当
 点在抛物线上运动时,猜想
点在抛物线上运动时,猜想 与
与 有什么数量关系,并证明你的猜想;
有什么数量关系,并证明你的猜想; 如图
如图 ,设点
,设点 ,问是否存在点
,问是否存在点 ,使得以
,使得以 ,
, ,
, 为顶点的三角形与
为顶点的三角形与 相似?若存在,求出
相似?若存在,求出 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,点
中,点 、
、 分别在边
分别在边 、
、 上,如果
上,如果 ,且
,且 ,那么下列说法中,错误的是( )
,那么下列说法中,错误的是( )
A. △ADE∽△ABC B. △ADE∽△ACD
C. △ADE∽△DCB D. △DEC∽△CDB
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,直线AB:
 交y轴于点A(0,1),交x轴于点B.直线x=1交AB于点D,交x轴于点E,P是直线x=1上一动点,且在点D的上方,设P(1,n).
交y轴于点A(0,1),交x轴于点B.直线x=1交AB于点D,交x轴于点E,P是直线x=1上一动点,且在点D的上方,设P(1,n).(1)求直线AB的解析式和点B的坐标;
(2)求△ABP的面积(用含n的代数式表示);
(3)当S△ABP=2时,以PB为边在第一象限作等腰直角三角形BPC,求出点C的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道:选用同一长度单位量得两条线段
 、
、 的长度分别是
的长度分别是 ,
, ,那么就说两条线段的比
,那么就说两条线段的比 :
: ,如果把
,如果把 表示成比值
表示成比值 ,那么
,那么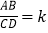 ,或
,或 .请完成以下问题:
.请完成以下问题: 四条线段
四条线段 ,
, ,
, ,
, 中,如果________,那么这四条线段
中,如果________,那么这四条线段 ,
, ,
, ,
, 叫做成比例线段.
叫做成比例线段. 已知
已知 ,那么
,那么 ________,
________, ________
________ 如果
如果 ,那么
,那么 成立吗?请用两种方法说明其中的理由.
成立吗?请用两种方法说明其中的理由. 如果
如果 ,求
,求 的值.
的值.
相关试题

