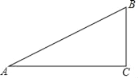
【题目】如图,Rt△ABC中,∠C=90°,∠A=30°.
(1)作线段AB的垂直平分线DE,垂足为点E,交AC于点D,要求用尺规作图,保留作图痕迹,标注有关字母,不要求写作法和证明;
(2)连接BD,直接写出∠CBD的度数;
(3)如果△BCD的面积为4,请求出△BAD的面积.
参考答案:
【答案】(1)详见解析;(2)30°;(3)8.
【解析】
(1)利用基本作图,作AB的垂直平分线即可;
(2)利用垂直平分线的性质得DA=DB,则∠DBA=∠A=30°,然后计算∠ABC-∠DBA即可;
(3)在Rt△BCD中利用含30度的直角三角形三边的关系得到DB=2CD,则DA=2CD,然后根据三角形面积公式得到S△ABD=2S△BCD=8.
(1)如图,DE为所作;
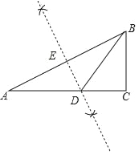
(2)∵DE垂直平分AB,
∴DA=DB,
∴∠DBA=∠A=30°,
∵∠ABC=90°﹣∠A=60°,
∴∠CBD=∠ABC﹣∠DBA=60°﹣30°=30°;
(3)在Rt△BCD中,∵∠CBD=30°,
∴DB=2CD,
而DA=DB,
∴DA=2CD,
∴S△ABD=2S△BCD=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】植树节期间,某单位欲购进A、B两种树苗,若购进A种树苗3棵,B种树苗5棵,需2100元,若购进A种树苗4棵,B种树苗10棵,需3800元.
(1)求购进A、B两种树苗的单价;
(2)若该单位准备用不多于8000元的钱购进这两种树苗共30棵,求A种树苗至少需购进多少棵?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E为矩形ABCD的边BC的中点,以DE为直径的⊙O交AD于H点,过点H作HF⊥AE于点F.
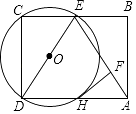
(1)求证:HF是⊙O的切线;
(2)若DH=3,AF=2,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值
(1)[(x﹣y)2+(x+y)(x﹣y)]÷2x,其中x=3,y=1.5
(2)(
 +m﹣2)÷
+m﹣2)÷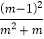 ,其中m=﹣
,其中m=﹣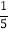 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校组织七年级175名学生参加社会实践活动,已知35座客车的租金为每辆320元,55座客车的租金为每辆400元.
(1)若学校单独租用这两种车,则各需多少元?
(2)若学校同时租用这两种客车共4辆(可以坐不满),而且比单独租用一种车节省租金,请你帮助该学校选择一种最节省租金的租车方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【阅读新知】
三角形中任何一边的平方等于其它两边的平方的和减去这两边与它们的夹角的余弦的积的两倍.
即:如图1,.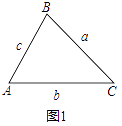
在△ABC中,已知AB=c,BC=a,CA=b,则有:
a2=b2+c2﹣2bccosA,b2=a2+c2﹣2accosB,c2=a2+b2﹣2abcosC
利用这个正确结论可求解下列问题:
例在△ABC中,已知a=2 ,b=2
,b=2  ,c=
,c= 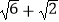 ,求∠A.
,求∠A.
解:∵a2=b2+c2﹣2bccosA,
cosA= =
= 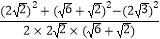 =
=  .
.
∴∠A=60°.
【应用新知】
(1)选择题:在△ABC中,已知b=ccosA,a=csinB,那么△ABC是( ).
A.等边三角形
B.等腰三角形
C.等腰直角三角形
D.直角三角形
(2)如图2,
某客轮在A处看港口D在客轮的北偏东50°,A处看灯塔B在客轮的北偏西30°,距离为2 海里,客轮由A处向正北方向航行到C处时,再看港口D在客轮的南偏东80°,距离为6海里.求此时C处到灯塔B的距离.
海里,客轮由A处向正北方向航行到C处时,再看港口D在客轮的南偏东80°,距离为6海里.求此时C处到灯塔B的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,抛物线y=ax2+bx+c与x轴交于两个不同的点A(﹣4,0),B(1,0),与y轴正半轴交于点C,tan∠CAB=
 .
.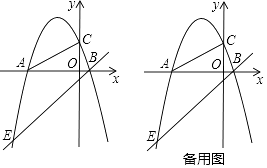
(1)求抛物线的解析式并验证点Q(﹣1,3)是否在抛物线上;
(2)点M是线段AC上一动点(不与A,C重合),过点M作x轴的垂线,垂足为H,交抛物线于点N,试判断当MN为最大值时,以MN为直径的圆与y轴的位置关系并说明理由;
(3)已知过点B的直线y=x﹣1交抛物线于另一点E,问:在x轴上是否存在点P,使以点P,A,Q为顶点的三角形与△AEB相似?若存在,请求出所有符合要求的点P的坐标;若不存在,请说明理由.
相关试题

