【题目】如图,点E为矩形ABCD的边BC的中点,以DE为直径的⊙O交AD于H点,过点H作HF⊥AE于点F. 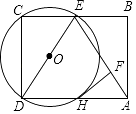
(1)求证:HF是⊙O的切线;
(2)若DH=3,AF=2,求⊙O的半径.
参考答案:
【答案】
(1)证明:连接OH,
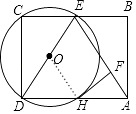
∵四边形ABCD为矩形,
∴CD=BA,∠C=∠B=90°,
∵E是BC的中点,
∴CE=BE,
∴△CDE≌△BAE(SAS),
∴ED=EA,
∴∠EDA=∠EAD,
∵OD=OH,
∴∠EDA=∠OHD,
∴∠EAD=∠OHD,
∴OH∥AE,
∵HF⊥AE,
∴HF⊥OH,
∵点H为⊙O上,OH为⊙O的半径,
∴HF是⊙O的切线
(2)解:连接EH,
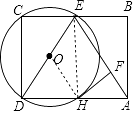
∵DE是⊙O的直径,
∴∠DHE=90°,
∵∠C=∠B=90°,
∴四边形HECD是矩形,
∴CE=DH,
同理:BE=AH,
∵CE=BE,
∴DH=AH=3,
∵CB∥AD,
∴∠BEA=∠EAD,
∵∠HFA=∠B=90°,
∴△FHA∽△BAE,
∴ ![]() ,
,
∴ ![]() ,
,
∴AE= ![]() ,
,
∴OD= ![]() DE=
DE= ![]() AE=
AE= ![]() ×
× ![]() =
= ![]() ,
,
∴⊙O的半径为 ![]() .
.
【解析】(1)连接半径OH,证明HF⊥OH即可;(2)连接EH,证明四边形HECD是矩形,则CE=DH,同理:BE=AH,再证明△FHA∽△BAE,列比例式为: ![]() ,求AE的长,由(1)知:DE=AE,且DE是直径,由此可得半径的长.
,求AE的长,由(1)知:DE=AE,且DE是直径,由此可得半径的长.
【考点精析】根据题目的已知条件,利用矩形的性质和切线的判定定理的相关知识可以得到问题的答案,需要掌握矩形的四个角都是直角,矩形的对角线相等;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了对学生进行爱国主义教育,某校组织学生去看演出,有甲乙两种票,已知甲乙两种票的单价比为4:3,单价和为42元.
(1)甲乙两种票的单价分别是多少元?
(2)学校计划拿出不超过750元的资金,让七年级一班的36名学生首先观看,且规定购买甲种票必须多于15张,有哪几种购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,C,D,E在Rt△MON的边上,∠MON=90°,AE⊥AB且AE=AB,BC⊥CD,BH⊥ON于点H,DF⊥ON于点F,OM=12,OE=6,BH=3,DF=4,FN=8,图中阴影部分的面积为( )

A. 30 B. 50 C. 66 D. 80
-
科目: 来源: 题型:
查看答案和解析>>【题目】植树节期间,某单位欲购进A、B两种树苗,若购进A种树苗3棵,B种树苗5棵,需2100元,若购进A种树苗4棵,B种树苗10棵,需3800元.
(1)求购进A、B两种树苗的单价;
(2)若该单位准备用不多于8000元的钱购进这两种树苗共30棵,求A种树苗至少需购进多少棵?
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值
(1)[(x﹣y)2+(x+y)(x﹣y)]÷2x,其中x=3,y=1.5
(2)(
 +m﹣2)÷
+m﹣2)÷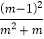 ,其中m=﹣
,其中m=﹣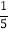 .
. -
科目: 来源: 题型:
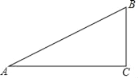
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,∠A=30°.
(1)作线段AB的垂直平分线DE,垂足为点E,交AC于点D,要求用尺规作图,保留作图痕迹,标注有关字母,不要求写作法和证明;
(2)连接BD,直接写出∠CBD的度数;
(3)如果△BCD的面积为4,请求出△BAD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校组织七年级175名学生参加社会实践活动,已知35座客车的租金为每辆320元,55座客车的租金为每辆400元.
(1)若学校单独租用这两种车,则各需多少元?
(2)若学校同时租用这两种客车共4辆(可以坐不满),而且比单独租用一种车节省租金,请你帮助该学校选择一种最节省租金的租车方案.
相关试题

