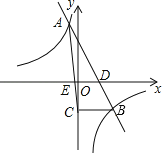
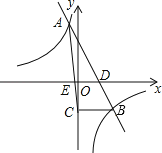
【题目】一次函数y=kx+b与反比例函数y=![]() 的图象相交于A(﹣1,4),B(2,n)两点,直线AB交x轴于点D.
的图象相交于A(﹣1,4),B(2,n)两点,直线AB交x轴于点D.
(1)求一次函数与反比例函数的表达式;
(2)过点B作BC⊥y轴,垂足为C,连接AC交x轴于点E,求△AED的面积S.
参考答案:
【答案】(1)y=﹣2x+2;(2)![]() .
.
【解析】
试题分析:(1)把A(﹣1,4)代入反比例函数y=![]() 可得m的值,即确定反比例函数的解析式;再把B(2,n)代入反比例函数的解析式得到n的值;然后利用待定系数法确定一次函数的解析式;
可得m的值,即确定反比例函数的解析式;再把B(2,n)代入反比例函数的解析式得到n的值;然后利用待定系数法确定一次函数的解析式;
(2)先由BC⊥y轴,垂足为C以及B点坐标确定C点坐标,再利用待定系数法求出直线AC的解析式,进一步求出点E的坐标,然后计算得出△AED的面积S.
解:(1)把A(﹣1,4)代入反比例函数y=![]() 得,m=﹣1×4=﹣4,
得,m=﹣1×4=﹣4,
所以反比例函数的解析式为y=﹣![]() ;
;
把B(2,n)代入y=﹣![]() 得,2n=﹣4,
得,2n=﹣4,
解得n=﹣2,
所以B点坐标为(2,﹣2),
把A(﹣1,4)和B(2,﹣2)代入一次函数y=kx+b得,
![]() ,
,
解得![]() ,
,
所以一次函数的解析式为y=﹣2x+2;
(2)∵BC⊥y轴,垂足为C,B(2,﹣2),
∴C点坐标为(0,﹣2).
设直线AC的解析式为y=px+q,
∵A(﹣1,4),C(0,﹣2),
∴![]() ,
,
解![]() ,
,
∴直线AC的解析式为y=﹣6x﹣2,
当y=0时,﹣6x﹣2=0,解答x=﹣![]() ,
,
∴E点坐标为(﹣![]() ,0),
,0),
∵直线AB的解析式为y=﹣2x+2,
∴直线AB与x轴交点D的坐标为(1,0),
∴DE=1﹣(﹣![]() )=
)=![]() ,
,
∴△AED的面积S=![]() ×
×![]() ×4=
×4=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中,对角线AC、BD交于一点O,AB=11cm,△OCD的周长为27cm,则AC+BD=_____________cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景
已知在△ABC中,AB边上的动点D由A向B运动(与A、B不重合),点E与点D同时出发,由点C沿BC的延长线方向运动(E不与C重合),连接DE交AC于点F,点H是线段AF上一点.
(1)初步尝试
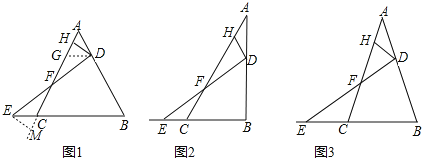
如图1,若△ABC是等边三角形,DH⊥AC,且点D,E的运动速度相等.求证:HF=AH+CF.
小王同学发现可以由以下两种思路解决问题:
思路一:过点D作DG∥BC,交AC于点G,先证GH=AH,再证GF=CF,从而证得结论成立;
思路二:过点E作EM⊥AC,交AC的延长线于点M,先证CM=AH,再证HF=MF,从而证得结论成立.
请你任选一种思路,完整地书写本小题的证明过程(如用两种方法作答,则以第一种方法评分);
(2)类比探究
如图2,若在△ABC中,∠ABC=90°,∠ADH=∠BAC=30°,且点D,E的运动速度之比是
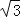 :1,求
:1,求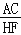 的值;
的值;(3)延伸拓展
如图3,若在△ABC中,AB=AC,∠ADH=∠BAC=36°,记
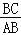 =m,且点D,E的运动速度相等,试用含m的代数式表示
=m,且点D,E的运动速度相等,试用含m的代数式表示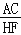 (直接写出结果,不必写解答过程).
(直接写出结果,不必写解答过程). -
科目: 来源: 题型:
查看答案和解析>>【题目】楼顶所在高度为18米,此时气球在楼顶正上方5米处,则气球的高度为___________米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若∠1=40.4°,∠2=40°4′,则∠1与∠2的关系是( )
A、∠1=∠2 B、∠1>∠2 C、∠1<∠2 D、以上都不对
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A的坐标为(2,5),则点A关于x轴对称点坐标为( )
A.(﹣2,5)
B.(2,﹣5)
C.(﹣2,﹣5)
D.(5,2) -
科目: 来源: 题型:
查看答案和解析>>【题目】若x﹣y=8,xy=10,则x2+y2=________
相关试题

